Maximum Likelihood Estimation(MLE)
August 19, 2021
오늘은 Maximum Likelihood Estimation(MLE)이라고 불리는 최대 우도법에 대해서 알아보도록 하겠습니다. MLE는 확률을 기반한 추정 문제를 해결할 때 사용되는 추정 방법입니다. 목차부터 살펴보도록 하겠습니다🙂
Category
- Definition of Maximum Likelihood Estimation(MLE)
- Likelihood Function and Log Likelihood Function
- Maximum Likelihood Estimation(MLE)
- MLE를 통한 모평균과 모분산 추정
- Summary
- Reference
Definition of MLE
MLE의 정의부터 살펴볼까요?? MLE는 으로 구성된 어떤 가우시안 정규 분포 probability density function, 에서 관측된 표본 데이터 집합을 이라 할 때, 이 표본들(을 통해 모수(파라미터) 를 추정하는 방법입니다. 위의 정의만 살펴 보았을 땐 이해가 잘 가지 않을 것입니다. 가 정규 분포라는 것에 유념하며 아래의 예시를 통해 정확히 무엇인지 알아보도록 하겠습니다.
우리는 어떤 가우시안 정규 분포 형태를 가진 probability density function, 을 기반으로 아래와 같은 데이터를 뽑았다고 가정해보겠습니다.
위의 데이터를 갖고 를 추정해보자!! 라고 하는 것이 바로 저희가 하고자 하는 일이며, 다시 한번 더 강조해서, 를 가우시안 정규분포라고 생각하고 추정하게 됩니다. 이 때, 가우시안 정규 분포를 결정할 때 필요한 모수(파라미터)에는 2가지가 존재하게 됩니다. 하나는 (mean)이고 다른 하나는 (variance)입니다. 즉, 정의에서 표현된 에서 은 (mean)을, 는 (variance)를 의미하게 되는 것입니다.
이 와 를 통해 정규 분포를 표현하게 되는데 우리는 어떤 parameter(와 ) 값을 가진 정규 분포로부터 해당 데이터를 뽑았는지 알고 싶어합니다. 이에, 후보 pdf 중 가장 그럴듯한 pdf를 뽑아내야하는데 우리가 사용할 방법이 바로 Maximum Likelihood Estimation입니다.
Likelihood Function and Log Likelihood Function
Maximum Likelihood는 각 데이터에 대한 likelihood 기여도를 구해서 모든 likelihood를 곱합니다. 이후 이 값이 최대가 되는 모수 값을 구해주게 되는데 그림으로 설명하겠습니다.
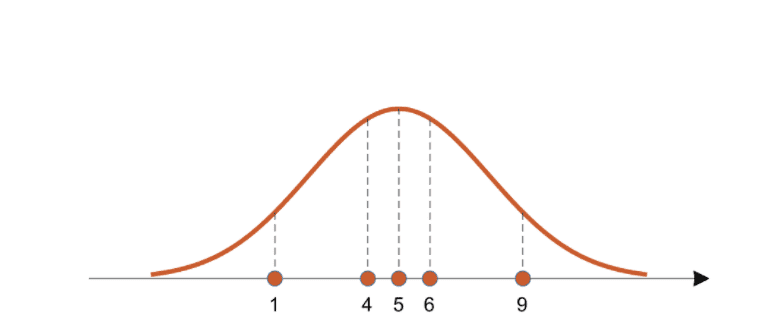
아래의 그림에 나와있는 1, 4, 5, 6, 9의 데이터는 우리가 아까 어느 정규 분포에서 sampling한 데이터이고 주황색 그래프는 수 많은 후보 pdf 중 하나를 그린 것입니다. 우리가 얻은 이 데이터가 주황색 그래프의 분포로부터 나왔을 가능도를 측정할 수 있는데 이를 likelihood라고 합니다. 수치적으로 가능도를 계산하기 위해서 각 데이터 샘플에서 후보 분포에 대한 높이(=likelihood 기여도)를 계산해서 다 곱하는 것입니다. 이를 우리는 likelihood function이라고 합니다. 수식으로 나타낸 다면 아래와 같이 나타낼 수 있습니다.
위의 는 데이터 를 어떤 특정 를 갖는 정규분포에서 sampling했을 확률을 의미합니다. 이 때, 위의 식인 likelihood function을 최대로 만드는 를 우리는 추정값 라고 합니다.
그리고 보통 자연로그를 이용해서 아래의 수식과 같이 log-likelihood function를 로 표기합니다.
Maximum Likelihood Estimation(MLE)
MLE는 위의 log-likelihood function이나 likelihood function을 Maximize하는 를 찾는 것입니다. log를 붙힐 수 있는 이유는 log함수가 monotonically increase(단조 함수)하기 때문입니다. 이에 likelihood function의 최대 값을 찾았을 때의 와 log-likelihood function의 최대 값을 결정하는 값이 같아 집니다.
또한, 최대 값을 찾는 경우에서 가장 일반적으로 많이 쓰이는 방법은 미분이나 편미분 했을 때의 값이 0인 지점을 찾는 것입니다. 그렇기 때문에 MLE에서도 값을 통해 편미분을 진행하고 그 편미분한 값이 0이 나오는 지점의 값을 구하게 됩니다.
보통 편미분을 했을 때, log 함수의 계산이 용이하기 때문에 log-likelihood를 사용하게 됩니다. log-likelihood function을 편미분했을 때의 수식은 아래와 같습니다.
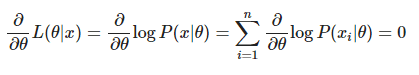
MLE를 통한 모평균과 모분산 추정
(mean)과 (variance)를 알지 못하는 정규 분포에서 표본 을 추출 했을 때, 해당 모분포의 평균과 분산을 추정해볼 수 있습니다.
정규 분포에서 각 표본들이 추출되므로 각 표본은 다음과 같은 likelihood 기여도를 갖습니다.
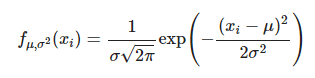
표본 모두 독립적으로 추출되었기 때문에(곱셈연산 진행) likelihood(우도)는 다음과 같습니다.
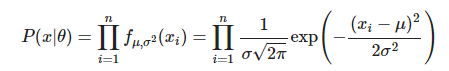
위의 likelihood function을 통해 log-likelihood function은 아래와 같습니다.
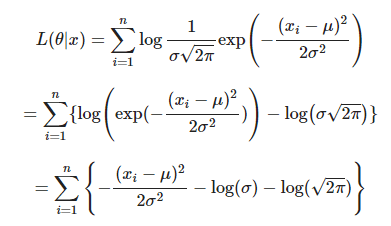
이제, log-likelihood function을 구하였습니다. 우리에게는 2개의 인 와 가 있기 때문에 각각에 대해서 미분해주고 log-likelihood function을 최대로 갖는 와 를 찾으면 됩니다. 우선, 부터 찾기 위해 를 에 대해 편미분 하겠습니다. 이후, log-likelihood function을 최대로 갖는 를 찾기 위해 를 에 대해 편미분 하겠습니다.
- 를 에 대해 편미분
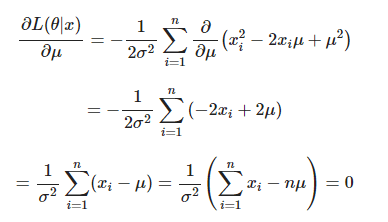
위의 결과에 따라 아래와 같은 결론을 얻을 수 있습니다. log-likelihood를 최대로 만들어 주는 모평균을 우리는 모평균의 추정량 라 하고 그 수식은 아래와 같습니다.
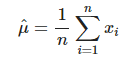
- 를 에 대해 편미분
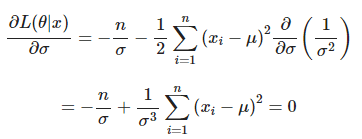
위의 결과에 따라 log-likelihood를 최대로 만들어주는 모분산을 우리는 모분산의 추정량 이라 하고 그 수식은 아래와 같습니다.
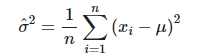
즉, 표본 데이터 을 통해 모평균과 모분산을 추정할 수 있는데 모평균의 추정 값은 표본들의 평균이며 모분산의 추정 값은 표본들의 편차 제곱의 평균입니다.
Summary
Maximum Likelihood Estimation은 표본들로 부터 가장 그럴 듯한 정규 분포의 를 추정하는 방법으입니다. 정의를 다시 한번 살펴보자면, 어떤 가우시안 정규 분포 probability density function, 에서 관측된 표본 데이터 집합을 이라 할 때, 이 표본들(을 통해 모수(파라미터) 를 추정하는 방법을 말합니다. 각 표본들()에 대한 proability(pdf 높이), 즉 likelihood 기여도를 모두 곱해서 likelihood를 구할 수 있는데 보통 log를 씌워 log-likelihood로 표현합니다. 이 log-likelihood를 최대화시키는 & 를 찾아야 하는데 이를 위해 편미분을 사용하고 편미분 값이 0이되는 지점의 값을 찾게 됩니다. log-likelihood를 최대화시키는 를 우리는 추정량이라고 하며 로 표기합니다.
다음 포스트에서 찾아 뵙겠습니다.
감사합니다😉
Reference
- MLE 설명, 사진 및 수식: https://angeloyeo.github.io/2020/07/17/MLE.html
