Matrix Multiplication based on Geometry
August 28, 2021
이번시간에는 머신 러닝 분야에서 많이 접할 수 있는 Matrix Multiplication에 대해 알아보도록 하겠습니다😎 Matrix Multiplication은 행렬곱이라 부르며 방정식을 풀 때 많이 사용합니다. 이 행렬곱을 벡터의 내적으로 보았을 때 어떻게 해석할 수 있는지 알아보도록 하겠습니다! 아래는 이번시간에 알아볼 Matrix Multiplication의 Category입니다.
Category
- Matrix Multiplication
- Linear Combination of Column Vector
- Linear Transformation in terms of Geometry
- Summary
- Terminology
- Reference
Matrix Multiplication
행렬곱은 아래와 같은 그림을 통해 진행됩니다.
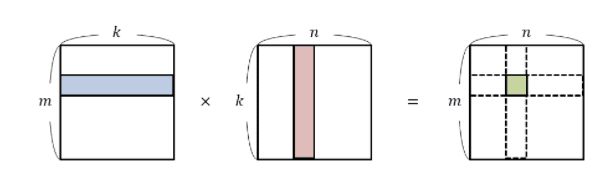
위의 그림은 행렬곱 과정의 일부를 잘 나타내고 있으며 수식을 통해 자세하게 나타내면 아래와 같습니다.
위의 수식을 보게되면 왼쪽 행렬에서는 행벡터를, 오른쪽 행렬에서는 열벡터를 사용해서 계산하는 것을 알 수 있습니다. 이에 행렬곱을 행벡터와 열벡터간의 내적으로 볼 수 있게 됩니다.
Linear Combination of Column Vector
또한 행렬곱을 열벡터의 선형 결합으로 불 수 있습니다. 이번에는 아래와 같은 수식을 보겠습니다.
위의 수식을 보게되면 Matrix Multiplication session에서 설명했던 것 처럼 왼쪽 행렬에 존재하는 두 개의 행벡터가 오른쪽에 존재하는 한 개의 열벡터와 내적되는 것을 볼 수 있습니다. 하지만 위의 식을 왼쪽 행렬에 존재하는 두 개의 열 벡터들의 선형결합으로 볼 수 있습니다.
위의 수식을 보면 알 수 있듯이 행렬과 벡터의 곱은 행렬을 구성하고 있는 두 열벡터의 선형결합을 표현한 것이라고 볼 수 있습니다.
Linear Transformation in terms of Geometry
위에서 행렬과 벡터의 곱이 열벡터의 선형결합으로 해석할 수 있다고 하였습니다. 뿐만 아니라 행렬과 벡터의 곱을 변형된 기저 벡터를 통한 벡터의 선형 변환으로 해석할 수 있습니다.
행렬 A를 통해 특정 벡터를 변환시키게 되면 다음과 같은 수식으로 표현할 수 있습니다.
(1,1)인 벡터를 행렬을 통해 변환하여 (-1,2)로 바꾼 것입니다. 기저 벡터를 (1,0)→(2,1), (0,1)→(-3,1)로 변형하였기 때문에 (1,1)→(-1,2)로 바뀐 것입니다.
우리는 이것을 선형 변환이라고 하는데 이에 대해 자세히 알아보도록 하겠습니다. 원래의 벡터 (1,1)은 기저 벡터인 (1,0)과 (0,1)을 1배와 1배의 합으로 표현한 것이기 때문에 (1,1)이라고 표기되었습니다. 아래 수식의 우항이 원래의 벡터 (1,1)을 의미하며 어떻게 (1,1)의 벡터가 기저벡터를 통해 나왔는지 좌항에서 볼 수 있습니다.
결국 각각의 기저벡터에 1배씩하여 합한 값이 (1,1)이 되어서 (1,1)로 표현한 것입니다. 아래는 (1,0)과 (0,1)을 기저벡터로 중심으로 1배씩하여 더한 (1,1)에 해당하는 좌표입니다.
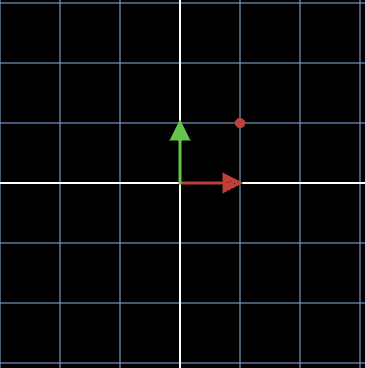
이제 우리는 선형 변환을 통해 위의 빨간점 (1,1)을 바꿔볼 것입니다. 원래의 기저벡터 (1,0)과 (0,1)만을 바꾸어 원래 있던 (1,1)을 변형할 것이며 (1,1)의 배율을 바꾸진 않습니다. 우리는 원래의 기저벡터 (1,0)과 (0,1)을 새로운 두 기저벡터 (2,1)과 (-3,1)로 바꿀 것입니다.
이렇게 기저벡터를 바꾸게 된다면 원래의 벡터(1,1)인 다음과 같은 과정을 통해 선형변환 됩니다.
위의 수식을 보게되면 바뀐 기저벡터를 (1,1)배하여 만든 열벡터가 (-1,2)이고 우리는 (1,1)이였던 원래 벡터가 (-1,2)로 선형변환 된 것을 확인할 수 있습니다. 아래의 그림은 선형변환한 벡터를 도식화하여 나타낸 것입니다.
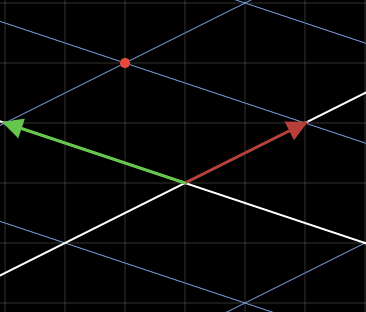
Terminology
- 기저 벡터(basis vector): n차원 공간에서 임의의 벡터를 표현할 수 있는 기준이 되는 벡터로 축방향을 가리키는 단위 벡터를 의미합니다.
Summary
우리는 지금까지 보았던 것처럼 행렬과 벡터의 곱을 열벡터의 선형 결합이라고 볼 수 있으며 우리는 이것을 또 변형된 기저벡터를 통한 열벡터의 선형변환이라고 볼 수 있습니다.
오늘 포스트는 이것으로 마치겠습니다!
감사합니다😉
