Weight Initialization

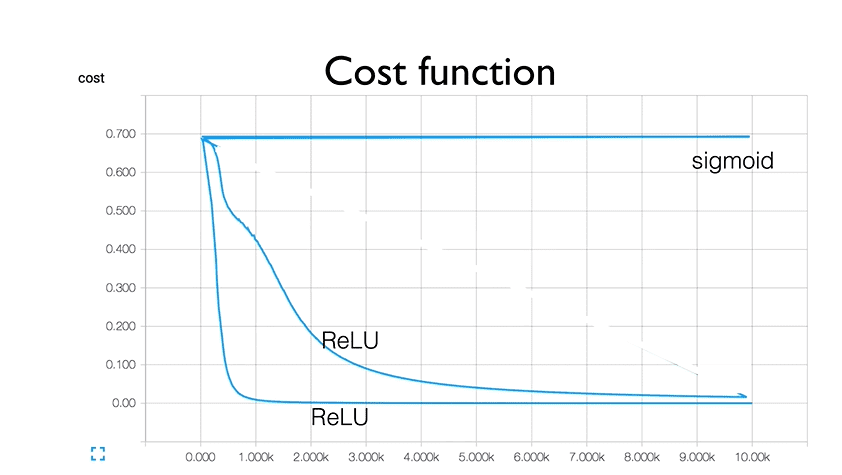
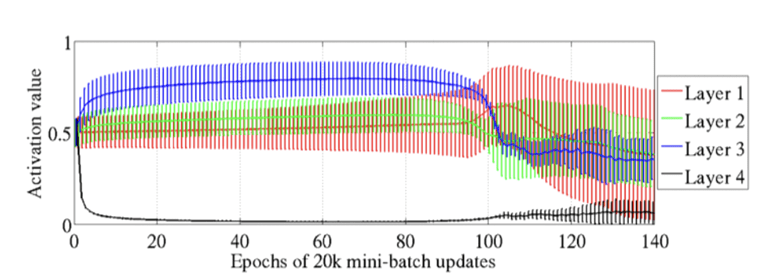
    이번 시간에는 weight initialization에 대해서 알아보도록 하겠습니다!😊 activation function을 sigmoid로 사용하게 되면 양쪽의 saturation area 때문에 gradient vanishing 현상이 생겨 학습이 잘 되지 않을 수가 있어서 ReLU나 Leaky ReLU를 사용하게 됩니다. 하지만 이 activation function을 잘 설정해도 아래 그림처럼 매번 학습되는 속도(cost가 떨어지는 속도)가 달라지거나 학습이 되지 않을 수 있는데 이는 weight initialization의 영향일 수 있습니다.

    이번 포스트의 카테고리는 다음과 같습니다.

Category

1. The Basic Concept of Weight Intilization
2. Weight Initialization Problems
3. Weight Initialization Methods
4. More Details about Xavier Initialization & He Initialization
5. Code
6. Summary
7. Reference

The Basic Concept of Weight Initialization

    우리가 모델을 알맞게 설정하고 activation function을 잘 선택해도 위에 봤던 그림처럼 매번 학습되는 속도(cost가 떨어지는 속도)가 달라지게 됩니다. 이는 weight initialization을 해주지 않고 weight 값을 random하게 주기 때문입니다. 따라서 어떻게 weight 값을 초기화해주며 종류에는 무엇이 있는지 알아보도록 하겠습니다.

Weight Initialization Problems

weight를 다음과 같이 초기화 해주게 되면 문제가 생깁니다.

① 작게 초기화하는 경우

1. 0.000.. 이되도록 weight를 너무 0에 가깝게 초기화 하는 경우
2. 많은 layer를 사용하면서 0에 가까운 값으로 weight를 초기화 하는 경우

② 크게 초기화하는 경우

위와 같은 경우에 왜 weight initialization problem이 생기는지 알아보겠습니다.

① 작게 초기화하는 경우

    작게 초기화 하는 경우, 우리는 다음과 같은 code로 weight를 초기화했다고 생각할 수 있습니다.

# Standard Gaussian Distribution which has standard deviation = 0.01
W = np.random.randn(fan_in,fan_out) * 0.01

    weight가 0.000.. 이되도록 weight를 너무 0에 가깝게 초기화 하는 경우 학습이 전혀 진행되지 않게 됩니다. 이유는 다음과 같습니다.

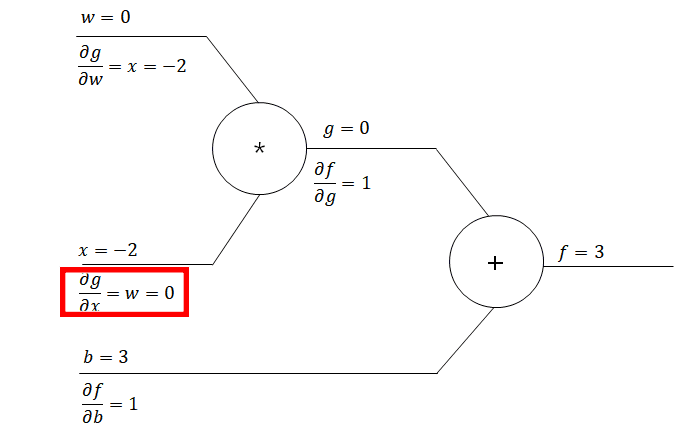
    ${\vartheta g \over \vartheta x} =w= 0.00..$이기 때문에 ${\vartheta f \over \vartheta x} = {\vartheta f \over \vartheta g} * {\vartheta g \over \vartheta x} = 0*1 = 0$이 됩니다. 이에 저 $x$와 연결되어 있는 모든 이전 node들의 gradient는 0이 되므로 gradient vanishing 현상이 생기게 됩니다. 이에 학습이 되지 않는 상황이 생기게 되므로 weight를 0으로 초기화하면 학습이 진행되지 않습니다.

    이제, 많은 layer를 사용하면서 0에 가까운 값으로 weight를 초기화 하는 경우를 살펴보겠습니다.

    activation function으로 tanh를 사용해서 학습을 진행하는 경우, 레이어를 통과하면 통과할 수록 모든 activation map의 값들이 0에 가까워지게 됩니다. 0에 가까운 weight들이 계속 곱해지면서 activation들이 0에 가까워지게 되고 tanh를 통과하면서 0으로 수렴하게 됩니다. 다시 이 값들이 0에 가까운 weight와 곱해지게 되면서 레이어가 깊어질 수록 모든 값들이 0으로 수렴되게 됩니다.

   위와 같은 현상이 진행된다면 back propagation step에서 gradient vanishing현상이 일어나게 됩니다.

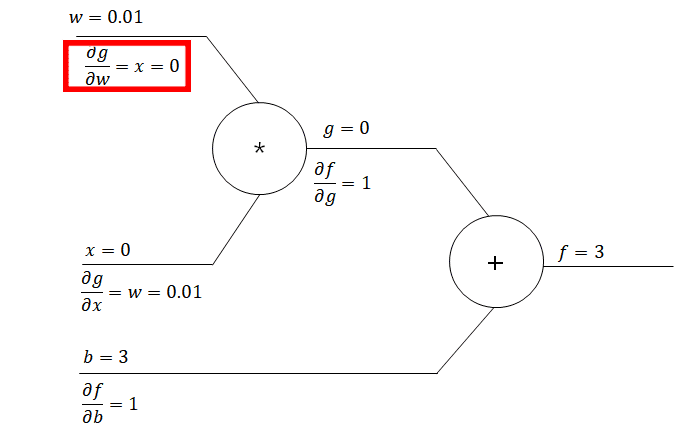
forward pass를 했을 때, 들어온 $x$값이 0이 된다면 backpropagation을 진행 할 때, upstream gradient와 local gradient를 곱할 경우 0이 됩니다. 이 과정은 아래의 수식과 같습니다

    위의 수식에서 ${\vartheta f \over \vartheta g}$ 은 upstream gradient이며 local gradient는 ${\vartheta g \over \vartheta w}$ 입니다. 이것은 하나의 layer만 보고 설명한 것인데 network를 전체로 설명하자면 다음과 같습니다.

    우리는 학습을 진행하기 위해 ${\vartheta loss \over \vartheta w}$ 를 구해야합니다. 이 값은 chain rule을 통해 구해 나가야하며 아래의 연산이 진행됩니다.

    위의 연산을 하기 위해서 upstream gradient와 local gradient(=$x$)를 곱해야하는데 local gradient인 ${\vartheta g \over \vartheta w}$가 0이 되기 때문에 update가 일어나지 않게 되는 것입니다. 이를 통해 알 수 있듯이, activation의 값의 분포를 보고 학습이 잘될 수 있는지 될 수 없는지 알 수 있습니다. activation 값 중 0이 많으면 local gradient가 0이되어 학습에 악영향을 미치니까요😉

② 크게 초기화하는 경우

    다음은 크게 초기화하는 경우를 살펴보도록 하겠습니다. 작게 초기화한 경우, 가우시안 표준정규분포의 표준편차를 1로 두었지만 지금은 1로 선언합니다.

# Standard Gaussian Distribution which has standard deviation = 1.0
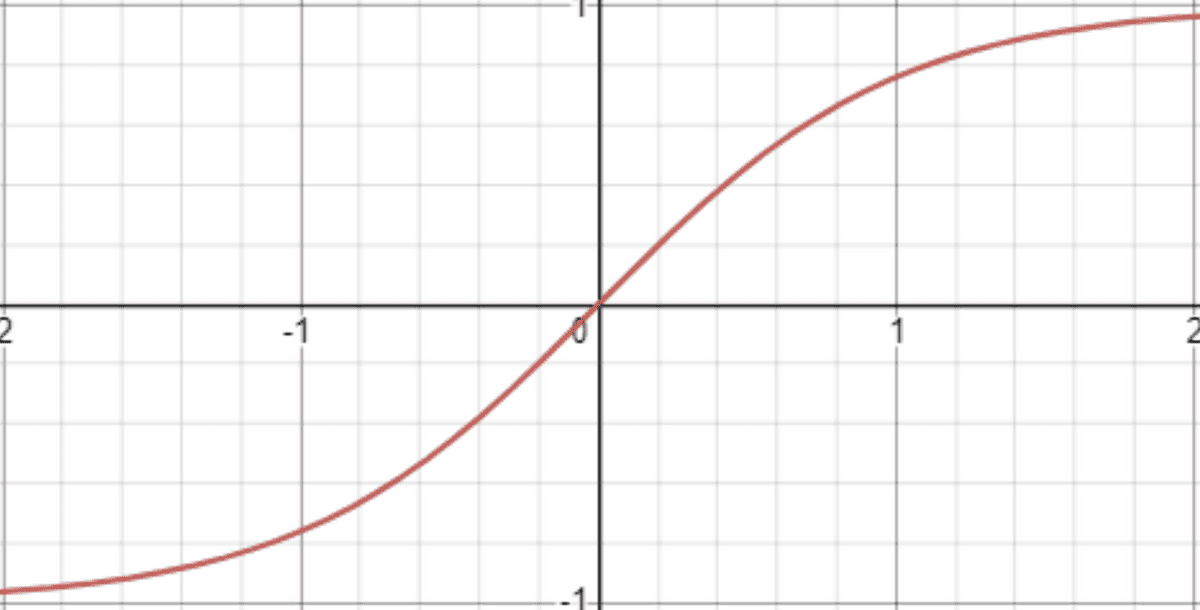
W = np.random.randn(fan_in,fan_out) * 1.0

    이 때, tanh activation function을 사용하게 되면 layer를 통과했을 때, activation이 -1과 1로 치중되게 됩니다. 그 이유는 아래와 같습니다.

    표준 편차가 큰 값으로 난수를 생성하여 weight를 초기화해주었습니다. 이후 $x$와 행렬곱을 진행하게 되면 극단적으로 작거나 큰 값을 가지게 됩니다. 이 값들이 tanh를 지나게 된다면 $x$축의 왼쪽과 오른쪽에 위치해서 tanh와 mapping되기 때문에 -1 이나 1값을 가지게 됩니다. 아래의 그림은 $y = tanh(x)$의 그래프 입니다.

Weight Initialization Methods

    weight를 초기화 하는 2가지 방법을 알아보도록 하겠습니다. 하나는 Xavier initialization이고 다른 하나는 He initialization 입니다. 먼저 Xavier initialization 부터 알아보도록 하겠습니다.

① Xavier initialization

    Xavier Initialization 은 uniform distribution 혹은 normal distribution으로 weight를 초기화할 때 다른 방법으로 초기화하게 되며 uniform distribution에서는 다음과 같은 범위를 사용합니다.

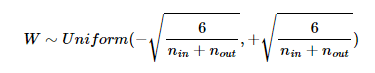
    하지만, 정규 분포로 초기화할 경우 평균이 0이고 표준 편차가 아래와 같은 $\sigma$를 가지도록 초기화 합니다.

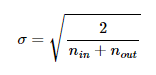
    따라서 해당 weight는 아래와 같은 정규 분포를 따르게 됩니다.

   코드로는 아래와 같이 작성해주면 됩니다.

# xavier initialization
W = np.random.randn(fan_in, fan_out) / np.sqrt((fan_in+fan_out)/2)

    위의 식을 보게되면 $N(0,1)$인 표준 정규 분포에서 sampling한 $W$를 $\sqrt{2/(in+out)}$으로 나누는 것을 볼 수 있습니다. 그 이유는 1의 표준 편차를 가진 분포를 $\sqrt {2 \over n_{in}+n_{out}}$의 표준편차를 갖는 분포로 바꾸기 위해서는 $\sqrt {2 \over n_{in}+n_{out}}$를 곱해주어야 하기 때문입니다.

    Xavier initialization은 non-linear activation function인 $tanh(x)$와 $sigmoid(x)$에서 좋은 성능을 보이지만 ReLU와 사용할 때 성능이 좋지 않습니다. 이에 ReLU를 사용할 땐 He initialization을 사용합니다.

② He initialization

    He initialization은 xavier initialization과 유사합니다. 정규 분포와 균등 분포 두가지로 나뉘게 되는데 He initialization는 xavier와 다르게 이전 층의 뉴런 수만 반영하고 다음 층의 뉴런 수를 반영하지 않습니다.

    weight를 uniform dstribution으로 초기화할 경우 아래와 같은 균등 분포 범위를 가지도록 합니다.

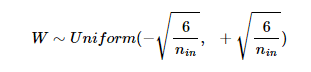
    하지만, 정규 분포로 초기화할 경우 아래와 같은 $\sigma$를 사용합니다

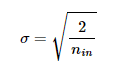
# He initialization
W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in/2)
# W = np.random.randn(fan_in, fan_out) * np.sqrt(2/fan_in)
# In Pytorch...
torch.nn.init.kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')

More Details about Xavier initialization & He initialization

    Xavier initialization은 tanh나 sigmoid형태의 비선형 함수에서 잘 동작합니다. 쉽게 설명하면 sigmoid와 tanh의 saturation영역으로 activation value들이 들어가지 않도록 설정해주기 때문입니다. 즉, sigmoid와 tanh의 linear 영역에 activation value들이 들어가도록 하면서 saturation에 빠지지 않도록 activation value를 조정합니다. 하지만 hidden layer가 3개가 넘어가 4개가 된다면 학습이 제대로 진행이 되지 않습니다. 아래의 그림은 sigmoid activation function을 통과한 각각의 layer의 activation value의 분포를 나타낸 것입니다.

    이런 현상이 일어나는 이유는 각 layer를 통과할 때마다 activation function을 통과한 acitivation value들의 분포가 linear한 영역에 있지 못하고 saturation영역에 들어가 분포가 흔들리기 때문입니다. 위의 각각의 그래프는 평균과 표준편차를 나타냅니다. 4개의 layer를 지나게 되면 sigmid activation을 통과한 activation value들의 ideal한 평균인 0.5에 현저히 못미치는 것을 볼 수 있습니다.

    이에 각 layer의 activation function을 통과한 activation value들의 분포를 모두 똑같이(mean과 standard deviation을 동일하게) 만들어주기 위해서 “이전 layer의 input 갯수($fan_{in}$)와 다음 layer의 output 개수($fan_{out}$)를 통해 weight를 초기화” 합니다. 이전 layer의 input개수를 통해서 설정하는 이유는 activation value들을 sigmoid나 tanh의 saturation 영역으로 보내지 않고 linear한 영역으로 가져가기 위함이고 output 개수를 통해 weight를 초기화하는 이유는 backpropagation과 관련이 있다고 합니다. 이렇게 해서 나온 initialization이 Xavier initialization입니다. Xavier initialization는 weight의 표준편차를 $\sqrt{2\over fan_{in}+fan_{out}}$이 되게 만드는데 이는 $**fan_{in}$과 $fan_{out}$의 조화평균**입니다.

    하지만 Xavier initialization은 아까 설명했던 것 처럼 sigmoid나 tanh와 같은 비선형 함수의 선형부분에 activation value들을 mapping시켜주어 forward와 backprop이 잘되게 해준 것이라 ReLU에는 잘 작동을 하지 않습니다. 이에 He initialization을 사용해줍니다.

    He intialization은 Xavier initialization의 표준편차에 $\sqrt{2}$를 곱해주어 weight의 분포를 좀 더 넓은 형태로 잡도록 도와줍니다. 왜냐하면 ReLU에서는 음의 영역에 있는 값들은 모두 activaion function을 지나게 되면 0이 되기 때문입니다. 이에 $\sqrt{2}$배 만큼 표준편차를 더 늘려주면서 layer를 통과할 때마다 양의 영역에 있는 activation 값들을 좀 더 펴주는 역할을 수행합니다.

    좀 더 다르게 해석해 본다면 직관적으로 봤을 때, ReLU는 음의 영역에 있는 activation value들을 없애므로써 입력을 반토막 낸다고 볼 수 있습니다. 이에 $**fan_{in}$에 2를 나눠서 마치 실제 입력의 반만큼만 입력으로 반영**된다고 생각할 수 있습니다. 이에 $fan_{in} \over 2$를 해준 것입니다.

    아래의 사진①은 He initialization 이 아닌 Xavier initialization을 사용했을 떄의 모습이며 사진②는 He initialization 을 사용했을 때의 activation value의 distribution입니다.

<사진①>

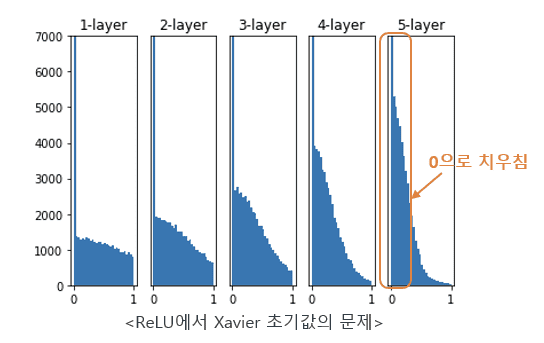
<사진②>

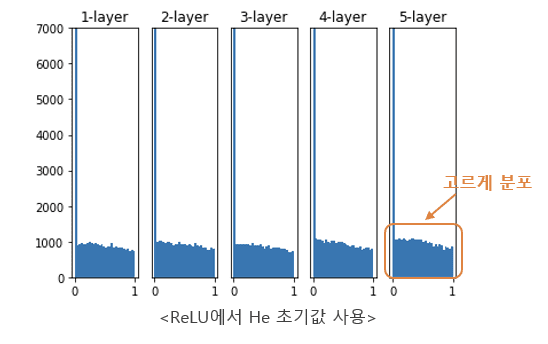
    해당 session과 관련된 내용(Xavier initialization 설명)은 아래 링크를 통해 들어가시면 보실 수 있습니다. 구글링을 하며 공부하던 중 감명깊게 읽은 블로그입니다👍

link: https://nittaku.tistory.com/269

Code

    Xavier, He initialization을 배우고 나서 GAN의 code에 직접 initialization을 적용해보았습니다. 두 개의 model을 설계하였는데 하나는 initialization을 그냥 random하게 준 것이고 다른 하나는 He initialization과 Xavier initialization을 통해 초기화 해주었습니다. Leaky ReLU를 사용한 부분은 He initilization을, tanh나 sigmoid를 사용한 부분은 Xavier initialization을 사용해주었습니다. 결과는 아래와 같습니다.

< Generator Loss >

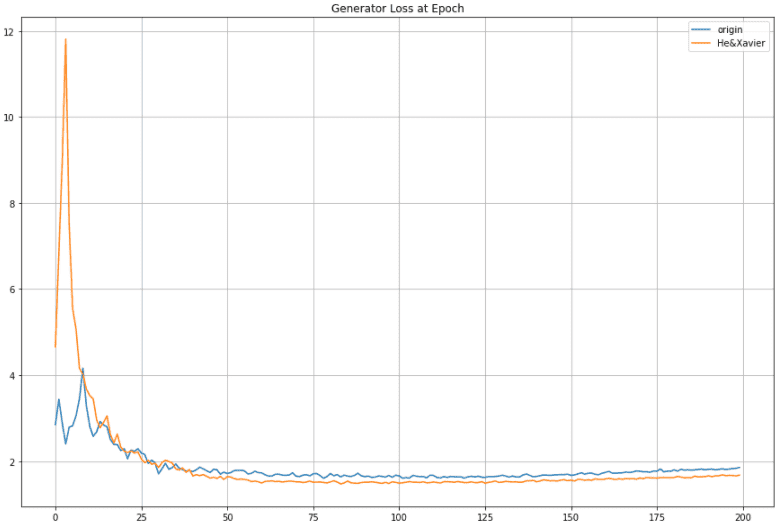
    위의 그래프는 initialization 해준 그래프(주황색)와 initilization을 해주지 않은 그래프(파란색) 입니다. 이것은 Generator loss로 initialization을 해준 그래프가 처음엔 loss가 엄청나게 뛰다가 빠르게 낮아지면서 initialization을 해주지 않은 그래프보다 loss가 작아진 것을 볼 수 있습니다. 급격하게 loss가 올라가 있는 부분은 discriminator의 학습이 압도적으로 잘되어 discriminator가 generator가 만든 image를 보고 fake image라고 잘 판단하였기 때문입니다. discriminator쪽에도 initialization을 적용해주었기 때문에 초반 epoch 에서 initialization을 적용한 generator의 loss가 initialization을 적용하지 않은 generator의 loss보다 엄청나게 큰 것 볼 수 있습니다. 또한, 초기화를 해준 generator가 안해준 generator 보다 학습이 급속도로 잘되는 것을 볼 수 있습니다.

< Discriminator Loss >

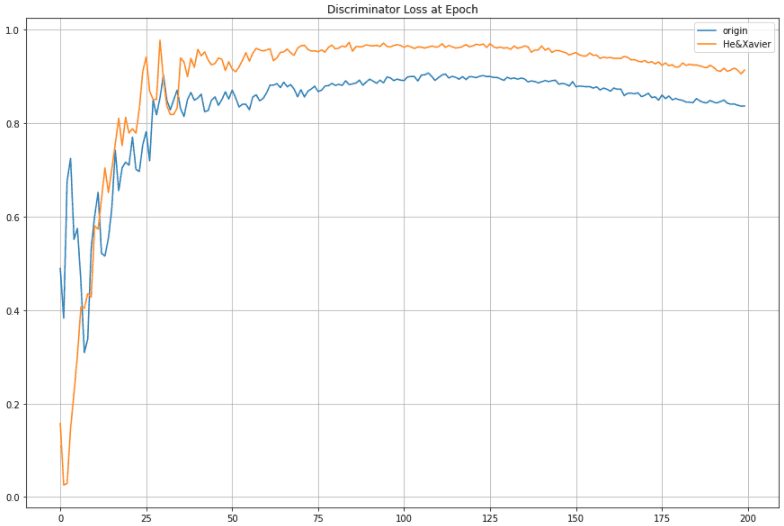
    initialization을 적용한 그래프가 적용하지 않은 그래프보다 초반 epoch에서 loss가 더 낮은 것을 확인해 볼 수 있습니다. 이것은 initialization을 통해 discriminator의 가중치가 잘 설정되었기 때문입니다. 하지만 epoch가 점점 경과되면서 initialization이 적용된 discriminator의 loss가 25 epoch 이후로 더 높은 것을 확인할 수 있습니다. 이것은 initialization이 적용된 Generator의 학습이 잘 되었기 때문입니다. Initialization을 적용한 discriminator의 loss가 initialization을 적용하지 않은 discriminator보다 높으므로 initialization을 적용한 discriminator가 Generator를 더 잘 학습된 것을 알 수 있습니다.

< Generator Accuracy >

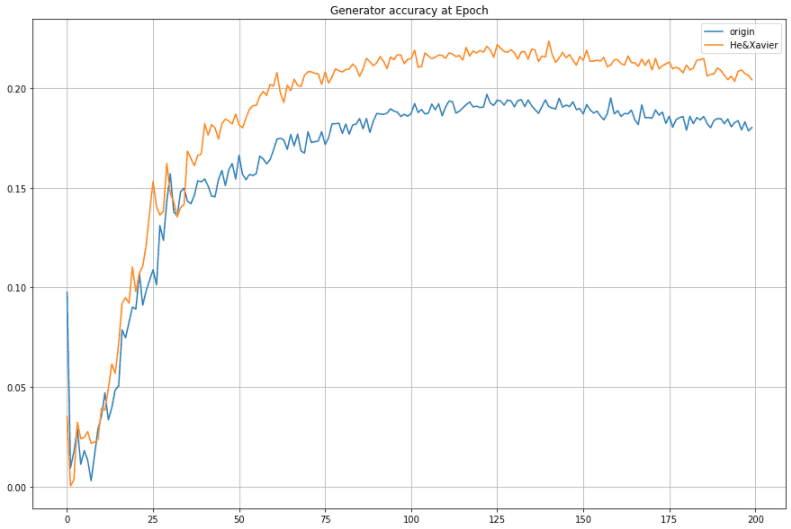
    따라서 이 실험을 통해 initialization을 사용하면 모델이 좀 더 빨리 학습될 뿐만 아니라 performance도 더 좋아진다는 것을 알 수 있었습니다.

위의 실험 결과에 대한 코드는 아래의 링크를 통해 볼 수 있습니다😉

link: xavier과 he initialization을 적용한 model VS origin model

Summary

1. Weight Intialization Problem은 weight가 너무 작거나 크게되면 문제가 발생합니다.
2. 각 레이어의 출력 분포를 확인하면 학습이 잘 되는지 확인할 수 있습니다. 만약 너무 극단적인 분포를 갖게 된다면(0으로 치중되거나 -1과 1로 퍼지는 현상) 학습이 잘 진행되지 않습니다. layer의 output 값들이 0으로 치중되는 경우, ${\vartheta loss \over \vartheta w} = {\vartheta loss \over \vartheta f} * {\vartheta f \over \vartheta g} * {\vartheta g \over \vartheta w}$를 구할 때 local gradient인 ${\vartheta g \over \vartheta w}$는 0이 됩니다(local gradient ${\vartheta g \over \vartheta w} = x=0$).이에 되면 ${\vartheta loss \over \vartheta w}$ 가 0 이되어 학습이 되지 않습니다. Layer의 output 값들이 -1 이나 1로 치중되는 경우, activation function의 saturation area의 gradient(around 0)가 chain rule에서 사용됩니다. 이에 ${\vartheta loss \over \vartheta w}$ 가 0이 되어 학습이 되지 않습니다.
3. xavier initialization은 fanin과 fanout을 사용하며 tanh, sigmoid에 적용합니다. He initialization은 fan_in을 사용하며 ReLU에 적용합니다.
4. He initialization은 Xavier initialization이 만들어주는 weight 분포의 $\sigma$(표준편차)보다 $\sqrt{2}$배 만큼 더 커서 activation value의 분포를 좌우로 더 늘려주게 됩니다.
5. Initialization을 사용하면 performance와 학습 속도가 올라간다!

Reference

• Xavier intialization: https://reniew.github.io/13/
• Xavier initialization 설명 및 사진 인용: https://nittaku.tistory.com/269
• He initialization 설명 및 사진 인용: https://excelsior-cjh.tistory.com/m/177