[Data Augmentation] Linear Transformation

August 29, 2021

이번 시간에는 image를 augmentation할 수 있는 방법인 Linear Transfromation에 대해서 알아보도록 하겠습니다!🙌 Linear Transformation에 대해서 알기 위해선 앞서 포스팅 했던 Matrix Multiplication에 대한 지식이 선행되기 때문에 보고와주세요~! 아래는 이번 포스팅의 Category입니다.

Linear Transformation

이전 포스팅을 보고 오셨더라면 행렬과 벡터의 곱이 두 열벡터의 선형결합…① 이라고 해석할 수 있다는 것을 이해하실 수 있을 겁니다.

\begin{pmatrix} 1 & 2\\3 & 4\\ \end{pmatrix} \begin{pmatrix} a \\ c\\ \end{pmatrix} = \begin{pmatrix} 1*a+2*c \\3*a+4*c \\ \end{pmatrix} =a*\begin{pmatrix} 1 \\3 \\ \end{pmatrix} + c*\begin{pmatrix} 2\\ 4\\ \end{pmatrix}

위의 식을 보게되면 ①이 무슨 말인지 이해하실 수 있습니다. 하지만 우리는 이것을 변형된 기저 벡터를 통한 벡터의 선형 변환이라고도 해석 할 수 있게 됩니다. 그럼 선형 변환은 무엇일까요?
먼저 선형 변환( $T$ )를 만족하는 두 개의 조건을 살펴보겠습니다.

임의의 벡터 $a, b$ 와 스칼라 $c$ 에 대하여 변환 $T$ 가 두 조건을 만족한다면 변환 $T$ 는 선형변환이라고 말합니다.

assets 2021 08 29 1

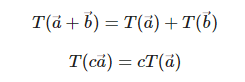
위의 변환 성질을 따르게 되면 어떤 임의의 벡터 $\begin{pmatrix} x \\ y\\ \end{pmatrix}$ 는 아래의 식을 만족하게 됩니다.

T(\begin{pmatrix} x \\ y\\ \end{pmatrix}) = T(x\begin{pmatrix} 1 \\ 0\\ \end{pmatrix}+y\begin{pmatrix} 0 \\ 1\\ \end{pmatrix}) = xT(\begin{pmatrix} 1 \\ 0\\ \end{pmatrix})+yT(\begin{pmatrix} 0 \\ 1\\ \end{pmatrix})

수식을 간단하게 하기 위해 아래의 수식처럼 표기하도록 하겠습니다.

\begin{pmatrix} 1 \\ 0\\ \end{pmatrix} = \hat i, \begin{pmatrix} 0 \\ 1\\ \end{pmatrix} = \hat j, T(\begin{pmatrix} 1 \\ 0\\ \end{pmatrix}) = \hat i_{new}, T(\begin{pmatrix} 1 \\ 0\\ \end{pmatrix})=\hat j_{new}

위의 식을 해석해 본다면 어떤 임의의 벡터 $\begin{pmatrix} x \\ y\\ \end{pmatrix}$ 를 선형 변환 시키게 되면 원래 기저 벡터 $\hat i$ 와 $\hat j$ 의 변형된 새로운 기저벡터인 $\hat i_{new}$ , $\hat j_{new}$ 의 $x$ , $y$ 배의 합으로 표현 가능하다는 말이 됩니다.

이 말은, 즉 원래의 기저 벡터를 새로운 기저 벡터로 바꿔(변형)주기만 한다면 선형변환을 구현할 수 있다는 말이 됩니다.

아래의 예를 살펴보겠습니다.

\begin{pmatrix} 1 & 0\\ 0 & 1\\ \end{pmatrix} \begin{pmatrix} 1 \\ 1\\ \end{pmatrix} = \begin{pmatrix} 1 \\ 1\\ \end{pmatrix}

위의 수식은 우항의 $\begin{pmatrix} 1 \\ 1\\ \end{pmatrix}$ 이 어떻게 계산된건지 알 수 있습니다. 좌항을 보게되면, $\begin{pmatrix} 1 \\ 0\\ \end{pmatrix}$ 과 $\begin{pmatrix} 0 \\ 1\\ \end{pmatrix}$ 을 기저벡터로 갖는 $\hat i$ 와 $\hat j$ 를 각각 1배하여 합한 것을 볼 수 있습니다. 이것은 행렬과 벡터의 곱이 두 열벡터의 선형결합으로 볼 수 있다는 관점(이전 포스팅에서 배웠죠?!)으로 본 것입니다.

\begin{pmatrix} 2 & -3\\1 & 1\\ \end{pmatrix} \begin{pmatrix} 1\\1\\ \end{pmatrix} =\begin{pmatrix} -1\\2\\ \end{pmatrix}

우리는 위에 있는 식의 좌항에 있는 행렬을 하나의 함수로 볼 수 있는데 이전에 설명했던 것처럼 행렬에 존재하는 하나의 열벡터를 기저벡터로 볼 수 있습니다. $\begin{pmatrix} 1 \\ 0\\ \end{pmatrix}$ 과 $\begin{pmatrix} 0 \\ 1\\ \end{pmatrix}$ 이 였던 원래의 기저 벡터에 $T$ 를 가해서 $\begin{pmatrix} 2 \\ 1\\ \end{pmatrix}$ 과 $\begin{pmatrix} -3 \\ 1\\ \end{pmatrix}$ 로 변형되었다고 생각해봅시다. 이렇게 변형한 새로운 기저벡터 $\hat i_{new}$ 와 $\hat j_{new}$ 에 1배씩하여 합하게 되는데 이 때 벡터는 $\begin{pmatrix} -1\\2\\ \end{pmatrix}$ 이 나오게 됩니다. 결국, $\begin{pmatrix} 1 \\ 1\\ \end{pmatrix}$ 인 벡터를 기저 벡터의 변형을 통해 각각 1배하여 더해서 $\begin{pmatrix} -1 \\ 2\\ \end{pmatrix}$ 로 변형했다는 것을 알 수 있으며 기하학적으로 아래의 그림들과 같습니다. 아래의 그림은 $\begin{pmatrix} 1 \\ 1\\ \end{pmatrix}$ 에 해당하는 그림입니다.

assets 2021 08 29 2

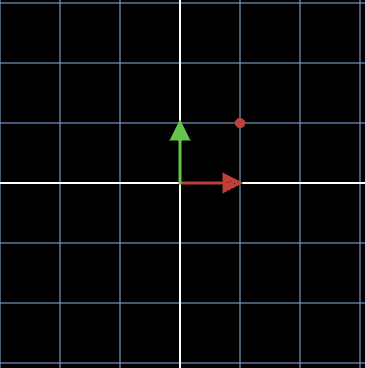
이렇게 $\begin{pmatrix} 1 \\ 1\\ \end{pmatrix}$ 에 해당하는 벡터에 $\begin{pmatrix} 2 & -3\\1 & 1\\ \end{pmatrix}$ 행렬을 통해 선형 변환을 시키게 되면 아래의 그림과 같이 변환되게 됩니다.

assets 2021 08 29 3

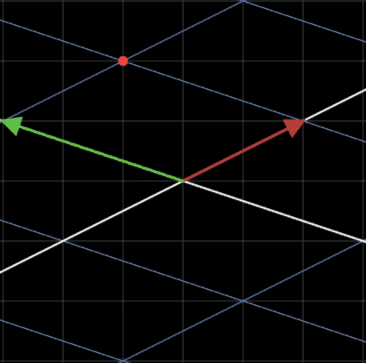
위 그림에서 초록색 벡터와 빨간색 벡터는 각각 새로운 기저 벡터를 의미하며 눈금에 찍한 좌표를 확인했을 때 각각 $\begin{pmatrix} -3\\ 1\\ \end{pmatrix}$ , $\begin{pmatrix} 2 \\1 \\ \end{pmatrix}$ 인 것을 확인할 수 있습니다.

즉, 원래의 기저벡터들의 상수배 합으로 표현 되었던 $\begin{pmatrix} 1 \\ 1\\ \end{pmatrix}$ 이 선형변환 후에는 새로운 기저벡터들의 상수배 합으로 표현되어 $\begin{pmatrix} -1\\2\\ \end{pmatrix}$ 가 나온 것입니다.