Linear Regression Model
August 12, 2021
이번 시간에는 Linear Regression Model에 대해서 알아보겠습니다. Linear Regression Model은 선형 회귀 모델로 다음과 같은 Hypothesis를 갖습니다.
Category
- The Basic Description of Linear Regression
- Total Code
- Pandas
- Matplotlib
The Basic Description of Linear Regression
Linear regression은 다음과 같은 hypothesis를 갖습니다.
위의 는 weight, 는 bias를 가리킵니다. 또한 loss function으로는 MSE 즉, Mean Squared Error를 사용하는데 MSE의 식은 아래와 같습니다.
이 loss function을 통해 weight에 대한 편미분을 구한 이후, weight를 update해주게 되는데 이를 라고 합니다. Linear regression에 대한 code는 아래와 같습니다.
Total Code
Linear regression을 ①numpy와 ②pytorch로 각각 구현하였습니다. numpy는 python이 지원하는 선형대수에 최적화된 라이브러리 입니다. python과 달리 matrix 연산이 편하게 되어 data science나 analaysis에 많이 사용됩니다.
반면, pytorch는 numpy와는 달리 GPU 연산을 지원하는 deep learning library입니다.
먼저, numpy로 구현한 모델을 보겠습니다.
# numpy
from google.colab import drive
import pandas as pd
import numpy as np
filename = '/content/drive/MyDrive/AI/1.Linear_Regression/ex1data1.txt'
df = pd.read_csv(filename, header = None)
df.head()
def hypothesis(theta, X):
return theta[0] + theta[1]*X
# borad casting 지원=> theta[1] * X
def cost_calc(m,theta, X, y):
return 1/(2*m) * np.sum((hypothesis(theta, X) - y)**2)
m = len(df)
def gradient_descent(theta, X, y, epoch, alpha, m):
cost = []
i = 0
while i < epoch:
hypo = hypothesis(theta, X)
theta[0] -= alpha*(sum(hypo-y)/m)
theta[1] -=(alpha * np.sum((hypo-y)*X))/m
cost.append(cost_calc(m, theta, X, y))
i += 1
return theta, cost
def predict(theta, X, y, epoch, alpha):
theta, cost = gradient_descent(theta, X, y, epoch, alpha, m)
return hypothesis(theta, X), cost, theta
theta = [0,0]
y_predict, cost, theta = predict(theta, df[0], df[1], 2000, 0.01)
%matplotlib inline
import matplotlib.pyplot as plt
plt.figure()
plt.scatter(df[0], df[1], label = 'Original y')
plt.scatter(df[0], y_predict, label = 'predicted y')
plt.legend(loc = "upper left")
plt.xlabel("input feature")
plt.ylabel("Original and Predicted Output")
plt.show()
plt.figure()
plt.scatter(range(0, len(cost)), cost)
plt.show()predict function의 cost variable은 matplotlib에서 cost가 어떻게 변하는지 보여주기 위해서 붙혀넣는 list이며, theta는 weight와 bias를 나타내고 hypothesis(theta, X)는 prediction을 의미합니다.
아래 코드는 pytorch로 구현된 코드입니다.
# pytorch
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)
x_train = torch.FloatTensor([[1],[2],[3]])
y_train = torch.FloatTensor([[2],[4],[6]])
W = torch.zeros(1, requires_grad = True)
b = torch.zeros(1, requires_grad = True)
optimizer = optim.SGD([W,b], lr=0.01)
nb_epochs = 1999
for epoch in range(nb_epochs + 1):
hypothesis = x_train * W + b
cost = torch.mean((hypothesis-y_train)**2)
optimizer.zero_grad()
cost.backward()
optimizer.step()
if epoch % 100 ==0:
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(epoch, nb_epochs,W.item(), b.item(), cost.item()))위의 두 개의 코드를 보면 알 수 있듯이 학습할 때 사용하는 코드는 크게 6가지 단계로 나누어 볼 수 있습니다.
- data 선언
- model parameter 초기화
- optimizer
- hypothesis
- cost 함수 선언
- cost 함수로 update
optimizer.zero_grad() → 가중치 초기화
cost.backward() → cost함수의 편미분 구하기
optimizer.step() → 구한 편미분으로 weight를 update
Pandas
위에서 numpy를 통해 구현하면서 data preprocessing 부분을 pandas로 처리하였습니다. 판다스에 대한 설명은 해당 포스트를 참고하시면 좋습니다. https://www.notion.so/Pandas-9863ad0661844d75bc08cab7c2c5ab66
Matplotlib
matplotlib은 다음과 같은 순서로 작성하면 기본적인 그래프를 만들 수 있습니다.
figure()→scatter()→legend()→xlabel()→ylabel()→show()
위의 순서대로 코드를 작성하게 되면 아래와 같이 작성할 수 있습니다.%matplotlib inline
import matplotlib.pyplot as plt
plt.figure()
plt.scatter(df[0], df[1], label = 'Original y')
plt.scatter(df[0], y_predict, label = 'predicted y')
plt.legend(loc = "upper left")
plt.xlabel("input feature")
plt.ylabel("Original and Predicted Output")
plt.show()Question
- torch.Tensor.item()은 무엇인가?
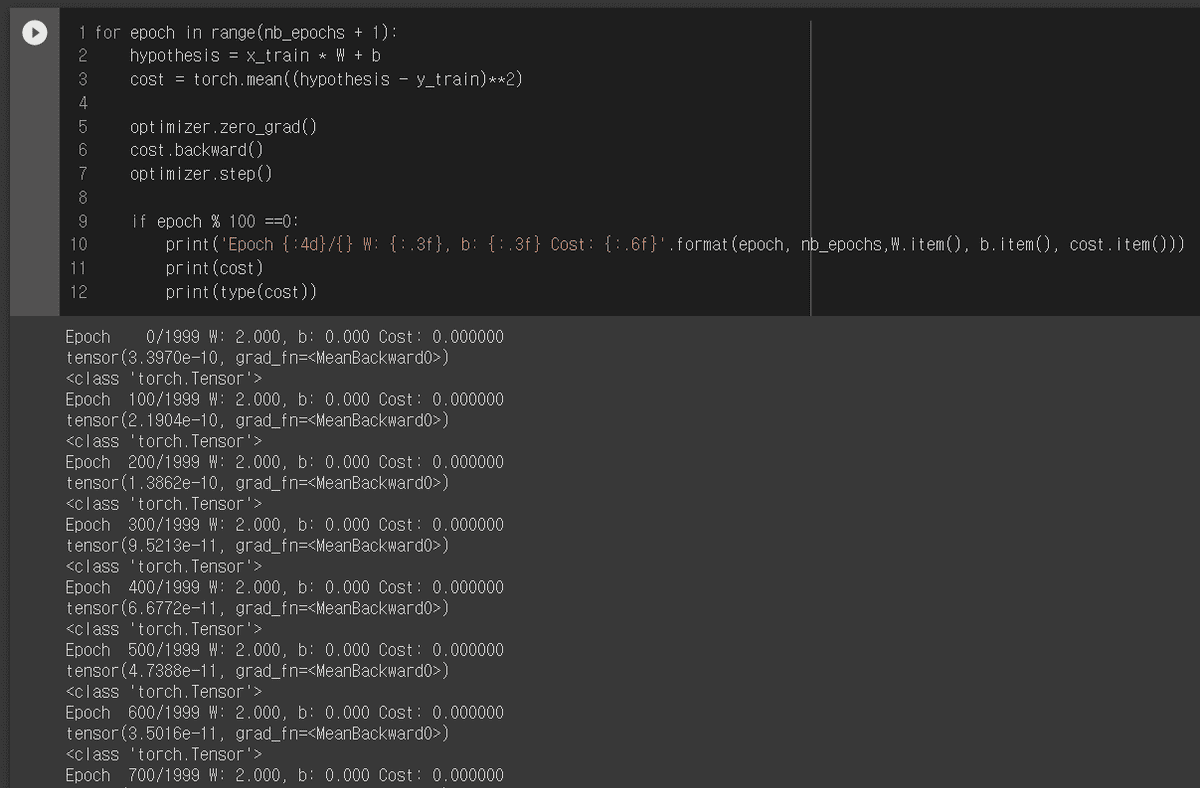
cost를 보게되면 type이 torch.Tensor이고 cost를 print시키게 되면 어떤 값 하나와, grad_fn이라는 값이 나오게 된다. 여기서 item()을 사용해주게되면 값만을 얻을 수 있습니다.
