Learning Rate Decay

    이번 시간에는 learning rate decay에 대해서 알아보도록 하겠습니다!😆 Learning rate는 hyperparameter중 가장 중요하다고 말할 수 있습니다. 이 learning rate $\alpha$에 따라서 학습속도가 결정되며 Global minimum으로 수렴할 수 있느냐를 결정하는 중요한 요소입니다. 그래서 오늘은 이 중요한 learning rate와 관련된 주제인 learning rate decay에 대해서 알아보도록 하겠습니다. 다음은 이번에 배울 learning rate에 대한 Category입니다!

Category

1. Learning Rate
2. Learning Rate Decay
3. The Kinds of Learning Rate Decay
4. Summary
5. Reference

Learning Rate

    이전 포스트 ’Fancier Optimization‘을 보게되면 다양한 Optimization algorithm들을 볼 수 있습니다. 기존에 사용했던 vanilla SGD는 각 차원(각 paramter를 하나의 차원으로 봅니다!)의 gradient를 고려하지 않기 때문에 Loss 값이 smooth하게 minimum으로 수렴하는 것이 아니라 zigzag로 수렴하게 됩니다. 즉, loss가 각 파라미터의 gradient값에 대한 민감도가 다르기 때문에 각 차원별로 이동하는 방향에 대한 크기에 달라지게되어 zigzag를 그리면서 수렴하게 됩니다. 또한, 현재의 gradient 값만을 생각해서 작동하기 때문에 saddle point나 local minimum에 걸리게 됩니다. 이에 만들어진 fancier optimization에는 vanilla SGD를 기반으로 만들어진 SGD+Momentum, AdaGrad, RMSProp, Adam 등등 많은 Optimization algorithm들이 존재합니다. 이 optimization기법의 원리는 여기에 기술되어 있으니 참고하시면 좋습니다😉

    하지만 이런 algorithm과 함께 동작하는 hyperparameter가 존재하는데요?! 바로 learning rate입니다. 이에 좋은 Optimization기법을 사용하는 것도 중요하지만 이와 함께 사용되는 learning rate 또한 중요하겠죠?? 기본적으로 learning rate는 아래와 같은 형태로 사용됩니다.

$W = W-\alpha{\vartheta Loss \over \vartheta W}$

    위의 수식은 vanilla gradient descent이며 $W$가 어떻게 update되는지 표현하고 있습니다. $Loss$를 $W$에 대해 편미분한 값(이것을 gradient라고 부르죠??👍)에 $\alpha$를 곱하고 $W$에 빼주어 update합니다. 여기서 $\alpha$가 learning rate를 의미하는데 이 learning rate는 수식에서 볼 수 있듯이 update될 gradient의 비율을 결정하게 됩니다.

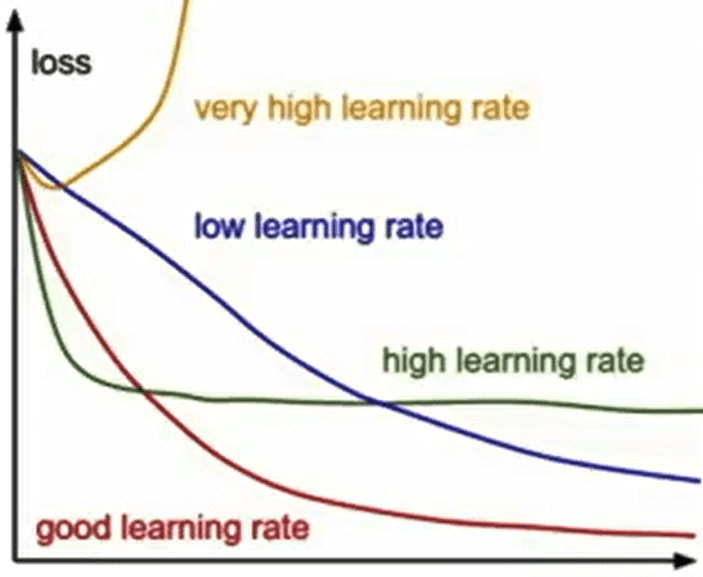
    위의 그림을 보게되면 learning rate의 정도에 따라 $Loss$가 어떻게 떨어지는지를 볼 수 있습니다. 이렇게 update 속도를 결정하고 있는 learning rate는 우리가 정해야할 가장 중요한 hyperparamter라고 할 수 있습니다. Random search나 다른 방법들을 이용해서 고정된 learning rate의 최적값을 찾을 수 있지만 우리는 learning rate decay를 사용하여 좀 더 효율적으로 학습을 진행시킬 수 있습니다.

Learning Rate Decay

    Learning rate decay란 학습이 진행될수록 learning rate를 점점 더 낮추는 것입니다. 왜 학습이 진행될 수록 learning rate를 점점 더 낮추어가는지 아래의 그림을 통해 알아보도록 하겠습니다.

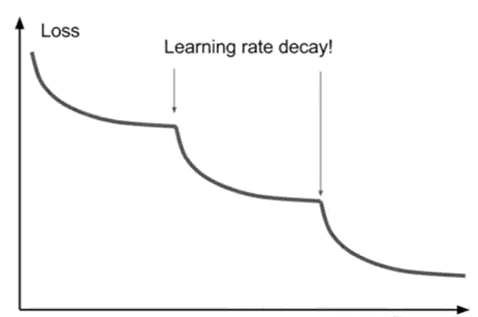
    위의 사진은 Resenet 논문에 나와있는 그림입니다. Loss가 특정 지점에서 수렴하는 듯 하더니 learning rate을 낮추니까 Loss가 떨어지는 것을 볼 수 있습니다. Loss가 일정 지점에서 수렴하는 이유는 learning rate가 높아 global minimum쪽으로 더 깊게 들어가질 못하기 때문입니다. 이 상황에서 learning rate를 줄여준다면 update되는 정도가 작지만 정밀하기 때문에 지속해서 global minium 쪽으로 내려갈 수 있습니다. 위의 그림을 좀더 입체적으로 보자면 아래의 그림처럼 나타낼 수 있습니다.

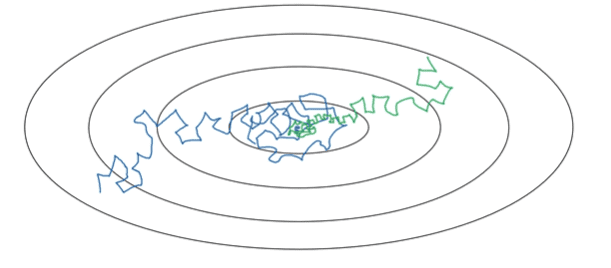
    파란색 선을 먼저 보겠습니다. small mini-batch 단위로 mini-batch gradient descent를 활용하게되면 노이즈를 갖고 minimum을 향해 가게 됩니다. 하지만 minimum 값에 정확하게 수렴하지 않고 그 주변을 돌아다니게 됩니다. 왜냐하면 고정된 learning rate를 사용하고 있고 서로 다른 미니배치들에 노이즈가 존재하기 때문입니다. 이 때, learning rate를 천천히 줄이게 되면 초록색 선처럼 초기 단계에서는 빠르게 학습하다가 점점 step이 작아지면서 minimum에 제대로 수렴할 수 있게 됩니다.

    하지만 learning rate decay는 Adam을 사용할 때보다 M-SGD(SGD Momentum)을 사용할 떄 더 많이 사용하며 부차적인 하라미터입니다. 일반적으로 학습 초기부터 learning rate decay를 고려하지 않습니다. 처음엔 learning rate decay를 생각하지않고 learning rate를 잘 선택하는 것이 중요합니다.

    따라서 learning rate decay를 설정하는 순서는 아래와 같습니다.

1. decay없이 학습을 실행합니다.
2. Loss curve를 살피고 decay가 필요한 곳이 어디인지 고려해봅니다.
3. learning rate decay를 적용합니다.

The Kinds of Learning Rate Decay

Learning rate decay는 다양한 방법들이 존재합니다.

① $\alpha ={1\over{1+decay~rate * epoch~num}}\alpha_0$

①은 epoch가 지날 때마다 분모가 커지면서 초기 $\alpha_0$의 값에 곱하여 learning rate를 작은 값으로 만들어 주게 됩니다.

② Exponential decay

Exponential decay는 지수형태로 되어있는 decay로 아래와 같은 수식을 갖습니다.

$\alpha=0.95^{epoch~num}\alpha_0$

    epoch가 지날 때마다 0.95가 계속 곱해지면서 초기 $\alpha$값인 $\alpha_0$가 계속해서 작아집니다.

③ Step decay

    epoch가 지날 때마다 계단처럼 learning rate를 감소시킵니다. 예를 들어, 20epoch가 지날때마다 0.1을 곱하여 $\alpha$값을 작게 만듭니다.

위에 존재하는 수식에서 hyperparameter는 $decay~rate$와 $\alpha_0$입니다.

Summary

1. Learning Rate Decay를 사용하게 되면 학습 알고리즘의 속도를 높일 수 있습니다.
2. 좋은 Learning rate를 선정한 이후, Loss curve를 보고 decay가 필요하다고 느껴지면 적용합니다. 따라서 다른 것 보다는 우선 순위가 낮습니다.

Reference

• learning rate decay: https://velog.io/@good159897/Learning-rate-Decay의-종류
• learning rate decay(including C2W2L09 Lecture): https://gaussian37.github.io/dl-dlai-learningratedecay/
• 사진 인용 및 설명: C2W2L09 Lecture