GAN

    이번 시간에는 GAN에 대해서 알아보도록 하겠습니다. GAN은 Generative Adversarial Networks를 의미하며 이것을 적대적 생성 신경망이라고 부릅니다. 본 포스트는 다음과 같은 Category로 이루어져 있습니다.

Category

1. Discriminate Model & Generative Model
2. Probability Density Function
3. The Principle of GAN
4. Code
5. The Improvement of GAN Loss Function
6. Summary
7. Many Kinds of GAN
8. Extension of GAN

Discriminate Model & Generative Model

    먼저, Discriminate Model과 Generative Model의 차이에 대해서 알아보겠습니다. Discriminate Model을 쉽게 설명하자면 input data가 어느 class에 속하는지 classify하는 모델입니다. 예를 들어, 개나 고양이 사진을 주면서 개인지 고양이인지 class를 분류하는 것입니다.

    반면, Generative Model은 데이터의 분포를 학습하여 새로운 이미지를 얻어낼 수 있는 모델을 말합니다. GAN의 경우, latent code를 주었을 때 그 code로 부터 이미지 데이터를 만들어 냅니다.

Probability Density Function

Probability Density Function이란?
  확률 밀도 함수로 확률 변수의 분포를 나타내는 함수입니다. 예를 들어 주사위의 확률 밀도 함수 즉, PDF를 살펴보겠습니다. 주사위의 눈이 나오는 경우의 수는 총 6가지이기 때문에 x축에는 주사위의 눈, y축에는 해당 주사위 눈이 나올 확률을 그리면 아래와 같습니다

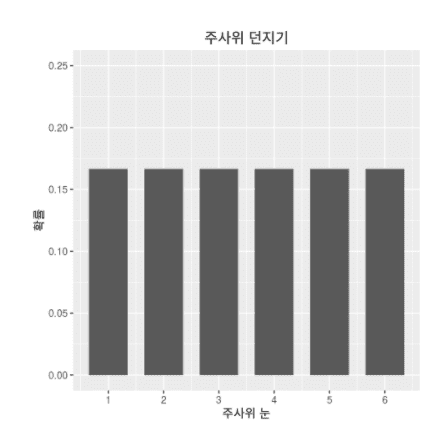
    위의 함수를 Probability Mass function이며 PDF의 불연속적 형태라고 보시면 됩니다. PDF(Probability Density Function) 는 연속적인 형태를 갖게 되는데 아래와 같은 분포를 PDF라고 합니다.

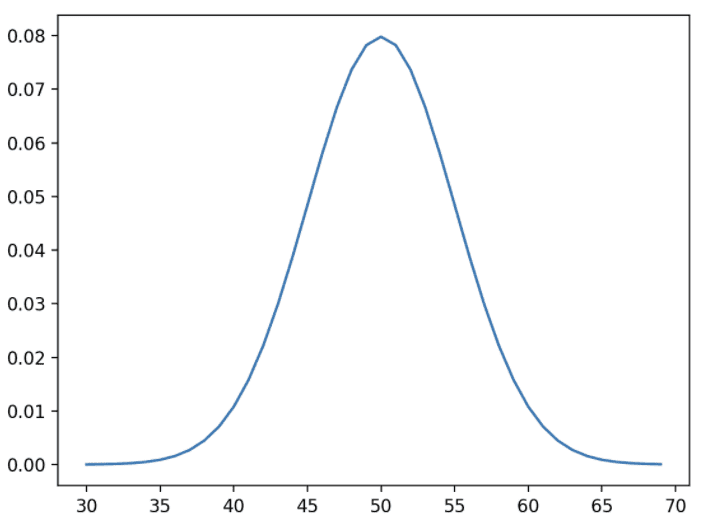
    다시 주사위의 눈에 대한 경우의 수를 나타내는 PMF로 돌아가서 이야기 해보겠습니다. 여기서 주사위의 눈의 종류는 6개이며 각각의 눈이 나올 확률은 $1\over 6$입니다.
  따라서 위와 같은 unifrom distribution을 이루게 되는데 이제 이 x를 주사위의 눈이 아닌 이미지 차원으로 늘리게되면 이미지의 분포를 볼 수 있다. 이때, x는 이미지가 되며 x를 $64*64*3$의 고차원 벡터로 생각할 수 있게 됩니다. 이미지들을 x축으로 한 PDF가 아래와 같다고 생각해보겠습니다.

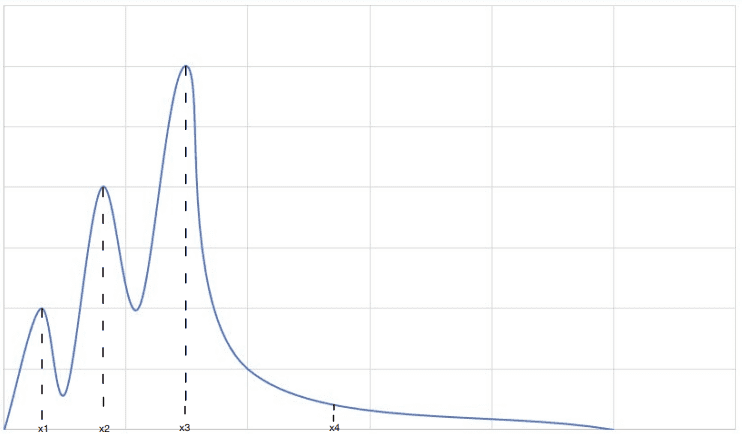
    만약 training dataset에 안경을 낀 남자가 적게 등장한다고 가정하고 그 안경을 낀 남자를 대표하는 고차원 벡터를 $x_1$의 벡터라 했을 때, 그 $x1$에 해당하는 확률밀도 값은 상대적으로 작게 나옵니다.
 이후, 안경을 끼지 않은 남자 및 안경을 낀 여자를 대표하는 고차원 벡터를 각각 $x_2$, $x_3$라하고 $x_3$의 확률이 $x_2$의 확률보다 작다고 할 때, 각각의 고차원 벡터가 대표하는 이미지의 갯수가 training data에서 차이가 난다는 이야기고 고차원 벡터($64*64*3$) $x_3$에 해당하는 이미지가 고차원 벡터($64 * 64 * 3$) $x_2$에 해당하는 이미지보다 많다는 것입니다. 즉, 여기서 고차원 벡터 x는 각각의 이미지에 mapping됩니다.
  이렇게 training data에 존재하는 이미지에 mapping되는 고차원 벡터를 만들어 PDF를 만들 수 있습니다. 이렇게 만든 PDF에 근사하도록 분포를 만들려는 model이 바로 위에서 배웠던 generative model입니다. Generative model은 해당 generative model에 의해서 만들어진 이미지의 분포가 데이터 셋에 대한 PDF에 근사하도록 만드는 것이 목표입니다. 즉, Generative model의 목표는 실제 학습 데이터의 분포와 model이 만들어낸 분포 간의 차이를 줄여주어 실제 학습 데이터의 분포에 잘 근사하도록 만들고자 하는 것입니다.

The Principle of GAN

    GAN에는 두가지 모델이 존재합니다. 그 모델은 바로 discriminator와 generator라고 불리는 model입니다. 위에서 Discriminative Model과 Generative Model의 정의를 간단하게 살펴보았었는데 바로 GAN의 discriminator는 Discriminative Model과 대응되고 generator는 Generative Model에 대응됩니다. 하지만 GAN의 최종적인 목표는 Generator라고 불리는 Generative model을 학습시켜서 이미지를 제작하는 것입니다. 이 목표를 위해 discriminator를 먼저 학습하게 됩니다.

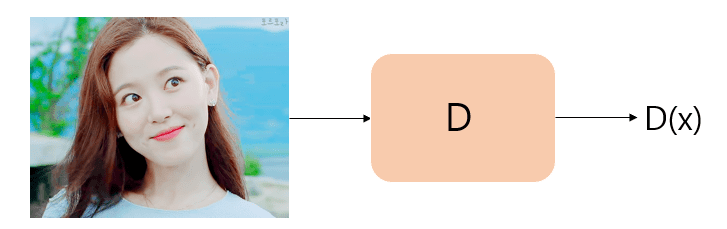
    Discriminator의 구조는 다음과 같이 동작합니다. Real picture를 discriminator에게 주게 되면 D(x)값을 반환하게 되는데 이것은 진짜 사진인지 가짜 사진인지를 판단한 value입니다. 이에 D(x)는 0~1의 값을 가지게 되는데, 1이라면 진짜 사진, 0이라면 가짜사진이라고 판단하는 것입니다. 이와 같이 두 개의 결과 값을 갖기 때문에 Binary Classifier이며 Binary Cross Entropy를 cost function으로 사용하게 됩니다.     이렇게 위와 같이 real image를 주면서 Discriminator를 학습시키게 됩니다. 이 때, Discriminator의 input은 $64*64*3$ image를 받게되고 binary classification이기 때문에 1차원의 output을 갖게 됩니다. 이후, 이 1차원의 값을 받아 sigmoid를 거쳐 0.5를 기준으로 binary classification을 수행합니다.

다음으로 Generator가 어떻게 동작하고 어떻게 학습되는지 살펴보겠습니다.

    위의 그림을 보게 되면 latent code z가 Generator로 들어가서 G(z)가 연산되게 됩니다. Generator가 만든 이미지이기 때문에 G(z)는 당연히 fake image가 되겠죠??
  G(z)는 Generator가 만든 사진으로 이 사진이 Discriminator로 들어가게 되는데, 이 때 Discriminator는 이 사진이 진짜 사진(real image)인지 아니면 Generator가 만들어낸 가짜 사진인지 판별해 내게 되는데 우리는 이 값을 D(G(z))라고 합니다. 따라서 이 D(G(z))의 값도 역시 D(x)의 범위와 같게 0부터 1까지의 값을 갖게 됩니다. 우리는 Generator가 만든 사진을 Discriminator가 진짜라고 인식하게 만들어야 하기 때문에 D(G(z))의 값이 1이 되도록 학습하여야 합니다.

    즉, Discriminator는 진짜 이미지를 보고서 진짜 이미지라고 판별할 수 있도록 학습이 되야되는 반면에, Generator는 Discriminator가 보고 진짜 이미지라고 판별할만한 G(z) 즉, Discriminator가 봤을 때 진짜 같은 fake image를 만들어야 하는 것입니다.

    위의 개념들을 통해서 우리는 다음과 같은 object function을 작성할 수 있습니다.

${min\atop G}{max\atop D}V(D,G)=E_{x~p_{data(x)}}[logD(x)]+E_{z~P_z(z)}[log(1-D(G(z)))]$

    GAN의 object function은 위와 같이 min max problem으로 표현할 수 있으면 위의 식을 최대화하는 D와 최소화하는 G를 찾으면 됩니다. 우선 Disciminator가 존재하는 첫번째 항부터 살펴보겠습니다.

    첫번째 항에서, $E_{x~p_{data(x)}}$는 real data distribution에서 sample x를 뽑아 Discriminator에게 넘겼을 때를 의미합니다. 예를 들어, 실제 학습데이터가 10만개의 사람이미지가 있다면 거기서 x값을 하나씩 뽑아온다고 생각하면 됩니다. Real image dataset에서 real image를 discriminator가 받았기 때문에 D(x)의 값은 1이 되도록 학습이 되어야 되고 그 때의 logD(x)는 log1이 되므로 0이 됩니다. 만약 Discriminator가 학습이 잘 되지 않아 D(x)가 1이 되지 않고 0이 되었다면 log(0)의 값은 -무한대로 가게 됩니다. 이에 Discriminator를 의미하는 D는 해당 식을 -무한대가 아닌 0으로 최대화시키는 방향으로 학습되어야 하기 때문에 위의 식을 최대화 하는 D를 찾아야 하는 것 입니다. 이제, Generator가 존재하는 두 번째 항을 보겠습니다.

    두번째 항에서,$E_{z~P_z(z)}$는 Gaussian Distribution에서 latent code z를 하나 sampling하여 D(G(z))연산을 진행한 것 입니다. 즉, random하게 z를 뽑아 Generator를 거쳐 fake image를 생성한 후 이것을 Discriminator에게 넘겨주어 진짜인지 아닌지 0~1까지의 값으로 표현해준 것입니다. 이 때, Discriminator 관점에서 보게되면 Discriminator는 G(z)가 fake image이므로 D(G(z))값이 0을 반환하는 것을 목적으로 합니다. 이 때 log(1)이 되므로 0이 됩니다. 따라서 첫번째항과 두번 째 항을 discriminator 입장에서 보게 된다면 D가 위의 object function을 0으로 최대화시켜야하며 이를 목적으로 학습되어야 합니다.

    하지만 Generator 입장에서 보게 되면 위의 object function을 최소화 시켜주는 Generator를 찾아야 합니다. Generator가 존재하는 두번 째 항만 살펴보게 되면 Discriminator를 잘 속였다면 두번째 항의 D(G(z))의 값은 1이 나와야하며 두번 째 항의 값이 log(0)이 됩니다. log(0)은 -무한대이므로 G는 위의 식을 -무한대로 최소화 시켜줄 수 있어야 합니다. 이에 우리는 위의 object function을 최대화 시키는 D와 최소화 시키는 G를 찾아야 합니다.

    따라서 위의 object function에 대해서 쉽게 요약해보면 다음과 같습니다. discriminator 관점으로 진짜 이미지를 진짜로, 가짜 이미지를 가짜로 학습해야합니다. 이렇게 학습하기 위해서 real image만 모여있는 dataset에서 뽑은 real image x에 대한 D(x)값은 1이 되어야합니다. 이에 첫번 째항은 log(1)이 되므로 0이되고 두 번째 항은 D(G(z))의 값이 0이 되어야 하므로 log(1)되어 0이 됩니다. 즉, discriminator는 위의 첫번째항과 두번째 항을 모두 0으로 만들기 때문에 위의 object function을 최대화합니다(D(x)나 D(G(z))가 1이 아니라 0이상 1미만이 된다면 log(소수) 형태가 되므로 음의 값이 나오기 때문에 0으로 최대화한다는 말을 사용합니다.).

    Generator 관점에서는 discriminator를 속여 fake image를 real image로 판단하게 만들어야 합니다. 이에 D(G(z))는 1이 되어야하고 log(0)가 되기 때문에 -무한대 방향으로 최소화 됩니다. 따라서 Generator는 objective function은 object function을 최소화해야 합니다.

이에 우리는 다음 과 같은 사실을 알 수 있습니다. D(x)는 0~1의 값을 갖게 되며, log(D(x))는 -무한대 ~ 0까지의 값을 갖게 됩니다.

Code

GAN을 구현한 pseudo code는 다음과 같습니다.

import torch
import torch.nn as nn
import torch.optim as optim

D = nn.Sequential(
	nn.Linear(784,128),
	nn.ReLU(),
	nn.Linear(128, 1),
	# Binary Classification
	nn.Sigmoid()
)

G = nn.Sequential(
	nn.Linear(100, 128),
	nn.ReLU(),
	nn.Linear(128, 784),
	nn.Tanh()
)

criterion = nn.BCELoss()
D_optimizer = optim.Adam(D.parameters(), lr=0.01)
G_optimizer = optim.Adam(G.parameters(), lr=0.01)

while True:
	# Training D
	loss = criterion(D(x), 1) + criterion(D(G(z)), 0)
	D_optimizer .zero_grad()
	loss.backward()
	D_optimizer .step()

	# Training G
	loss = criterion(D(G(z)), 1)
	G_optimizer.zero_grad()
	loss.backward()
	G_optimizer .step()

    위의 코드에서 보게되면 D는 discriminator를 G는 generator를 의미합니다. 이에 D는 이미지를 받아서 1차원 형태의 output을 뽑아내게 되고 G는 latent code를 받아 이미지를 만들게 됩니다. 학습할 땐, 이 이미지를 discriminator에게 전달해주어 discriminator가 실제 이미지라고 생각할 수 있도록 generator를 훈련시킵니다.

    loss function으로는 nn.BCELoss를 사용해서 D를 학습하게 됩니다. Discriminator를 학습시킬 경우, D(x)를 넣었을 땐 무조건 1이나와야 하므로 criterion(D(X),1)을 넣어서 해주고, D(G(Z))를 넣었을 땐 가짜이미지 이므로 0이라고 학습해야 합니다. 이에 이 부분의 loss를 작성할 땐 criterion (D(G(Z)),0)을 사용합니다.

    또한, 실제로 image를 학습시킬 땐 -1~1사이로 normalization을 해줘서 진행하기때문에 진짜 이미지의 범위를 맞춰주기 위해서 G에 tanh()를 넣었는데 사용하지 않아도 된다고 합니다. Generator를 학습하는 과정에 있어서 -1보다 작은 값, 1보다 큰 값을 내보내면 안된다는 것을 학습하기 때문에 tanh의 사용을 해도되고 안해도 됩니다.

    D와 G는 한 epoch마다 같이 학습하게 되지만 generator를 학습할 때는 discriminator의 parameter를 고정시켜주어야 합니다. 이때, D(G(Z))와 1 차이 값을 계산해서 backpropagation하되 discriminator에 있는 weight와 bias는 학습안하고 generator부분에서만 학습이 이루어지도록 합니다. 이에, G를 training할 때, g_optimizer.step()만을 사용해서 discrminator는 학습을 시키지 않고 generator만 학습하게 됩니다. 여기서 중요한 것은 위와 같은 방법을 사용하면 generator가 학습 될 때, discriminator에 대한 backpropagation은 이루어지지만 학습이 되지는 않는다는 것입니다.

GAN code는 아래의 링크를 통해 확인할 수 있습니다.
GAN(Generative Adversarial Network): https://colab.research.google.com/drive/1h7FtHwJw34w0EEQiTj4izzckMR1bL7Bn?usp=sharing

The Improvement of GAN Loss Function

    위에서 저희는 GAN의 object function을 살펴보았습니다. 다시 그 식을 보자면 다음과 같습니다.

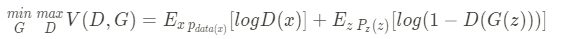
    이 식에서 Generator인 G가 들어가 있는 부분을 살펴보겠습니다. 위 식의 두번 째 항을 보게되면 $log(1-D(G(z)))$라고 되어 있는데 이것을 그래프로 그려보게 되면 아래의 그림과 같이 나오게 됩니다.

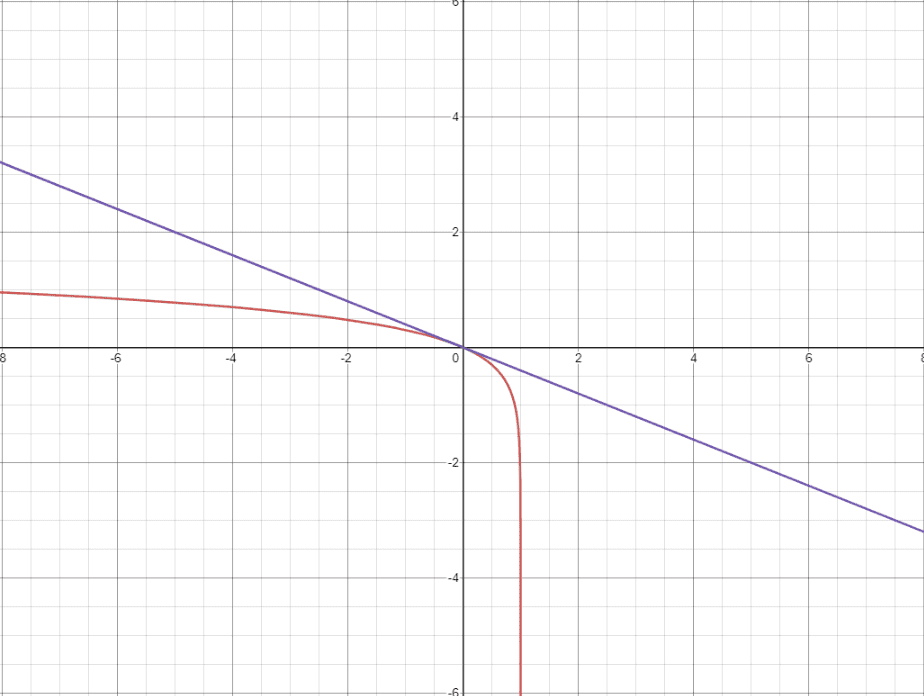
    위의 그래프를 보게되면 빨간색 그래프는 $log(1-x)$이고 보라색 그래프는 $log(1-x)$일때 $x=0$에서의 기울기 입니다. 우리가 G를 생각해보면 D(G(z))의 초기 값은 항상 0일 수 밖에 없습니다. 왜냐하면 genrative model은 처음에 형편 없는 그림을 만들기 때문에 discriminator는 generator가 첫번째로 만든 모델이 fake image라고 판단하게 됩니다.

    이에 $log(1-D(G(z)))$에서 $D(G(z))$는 0이 됩니다. 하지만 $log(1-x)$ 그래프에서 $x=0$일 때 gradient가 낮기 때문에 이 부분에서 update가 빠르게 되지 않습니다. 이에 초기 상황에서 빨리 벗어나기 위해 위와 같이 G가 $log(1-D(G(z)))$를 최소화하는 것이 아니라 $log(D(G(z)))$를 최대화 하는 방향으로 학습하게 됩니다. log(x) 그래프는 아래와 같습니다.

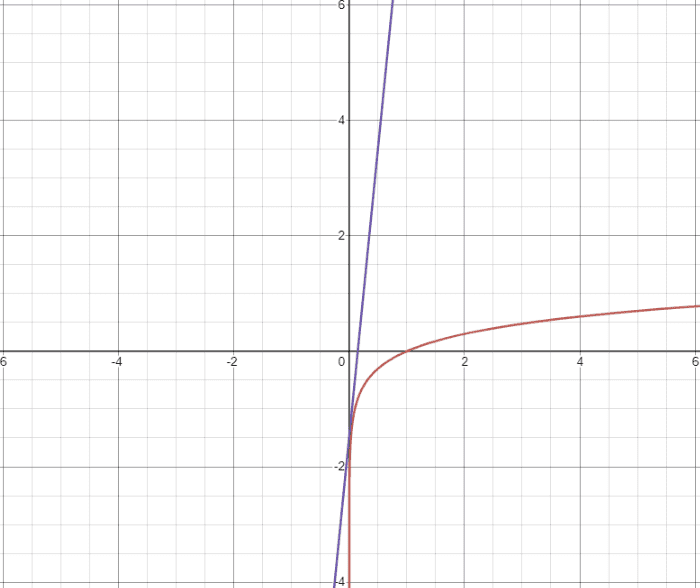
    $log(1-x)$와는 달리 $log(x)$는 $x=0$에서 gradient가 엄청나게 큰 것을 볼 수 있습니다. 이에 학습이 더 원할하게 진행되게 됩니다. 이에 $log(x)$를 사용하게 되는데 사실, 위의 The code of GAN에서는 해당 원리를 사용하여 code를 구현한 것입니다. nn.BCELoss 를 사용한 것이 바로 해당 원리를 사용한 것입니다. Binary cross entropy의 수식은 $-(ylog(H(x)+(1-y)(1-H(x)))$입니다. object function 안에 있는 Generator를 $log(1-x)$에서 $log(x)$로 바꾸려면 Binary cross entropy를 사용하면 됩니다.

${min\atop G} E_{z~p_{z}(z)}[-ylogD(G(z))-(1-y)log(1-D(G(z))]$ → $in~y=1$ → ${min \atop G} E_{z~p_z(z)}[-logD(G(z))]$ → ${max \atop G} E_{z~p_z(z)}[log(D(G(z))]$

    위에서 볼 수 있듯이 nn.BCELoss를 사용하여 정답 label을 1로 두게 됩니다($y=1$). 왜냐하면 코드를 작성할 때, nn.BCELoss(D(G(z)),1) 이라고 작성하는데 여기서 label 값을 1로 설정해주기 때문입니다. 그 결과, $-log$항만 남게 되는데 이 -를 삭제해주면 G가 $-log$ 식을 최소하는 것에서 $log$를 최대화하는 것으로 바뀌게 됩니다. 이에 Generative model의 학습 속도가 굉장이 빨라지게 됩니다.

    처음에 0에서의 기울기가 거의 -무한대에 가깝게 되어 parameter가 학습될 때 gradient가 엄청 뛰게 되어 발산한다고 생각할 수도 있습니다. 하지만 이것은 initialization기법을 사용하여 그 값을 조정 해주거나 lr을 조정해주게 되면 해당 문제를 해결할 수 있습니다.

Summary

   이번 포스트에서 GAN을 이해하기 위한 수학적 지식과 원리, code를 알아보았습니다. GAN은 real data의 분포와 Generative model이 만드는 distribution 사이의 차이를 최소화 시켜 real data와 비슷한 어떤 output을 만들어주는 Generative model이라고 정의할 수 있습니다. 따라서, GAN이 이론적으로 잘 동작하는 이유는 실제로 서로 다른 확률 분포간의 차이를 줄여주기 때문에 실제 generator가 진짜에 가까운 이미지를 만들 수 있기 때문입니다.
Object function은 ${min\atop G}{max\atop D}V(D,G)=E_{x~p_{data(x)}}[logD(x)]+E_{z~P_z(z)}[log(1-D(G(z)))]$이며 BCELoss를 통해 학습 초기에 gradient가 작아 빠르게 update가 되지 않았던 것을 gradient를 높여주므로써 학습 초기에 빠른 학습이 진행 될 수있습니다. 다음 시간엔 GAN의 종류에 대해서 배워보도록 하겠습니다.

감사합니다😉

Reference

• 그래프 그려주는 사이트: https://www.desmos.com/calculator/’
• 1시간 만에 gan 완전히 정복하기: https://www.youtube.com/watch?v=odpjk7_tGY0&t=206s
• pytorch library 공부: https://tutorials.pytorch.kr/beginner/dataloadingtutorial.html