[Data Augmentation]Affine Transformation

August 30, 2021

이번 시간에는 저번 시간의 [Data Augmentation] Linear Transformation에 이어서 Affine Transformation에 대해서 알아보겠습니다!👍 이전 시간에 Linear Transformation은 기저벡터의 변형을 통해 이루어지는 것을 알 수 있었습니다. 하지만 이전시간에 배웠던 개념으로는 translation(이동)을 설명할 수 없습니다. 왜냐하면 벡터는 눈에 보이지 않는 추상적인 개념이며 같은 차원에서의 설명이 불가하기 때문입니다. 그래서 오늘은 translation(이동)을 설명할 수 있는 Affine Transformation에 대해서 알아보도록 하겠습니다.

Relationship Between Dots and Vectors

우선 Affine transformation을 설명하기 전에 점과 벡터의 관계에 대해서 명확하게 할 필요가 있습니다. 이전 포스팅인 [Data Augmentation] Linear Transformation에서 인용한 사진을 보게 되면 시각화하기 위해 그려진 벡터를 볼 수 있습니다. 하지만 이것은 어느 한 벡터 공간 안에 볼 수 없는 벡터를 시각화 하기 위해 원점에서 부터 뻗어 그린 것에 불과합니다. 즉, 벡터는 우리가 느끼거나 볼 수 있는 물체가 아니라 무엇인가를 운반하고 밀게 되는 수단입니다. 벡터와 같이 벡터 공간도 무엇인가를 움직이는 힘이 작용하는 공간일 뿐 어떤 물체를 표현하는데 사용하는 것은 아닙니다.

이에 벡터를 통해서는 어떤 물체를 표현하지 못합니다. 이에 물체를 표현하기 위해서 가장 기본적인 점을 이용하게 됩니다. 벡터에 점이라는 개념을 추가해서 창조한 새로운 개념의 공간을 아핀(Affine) 공간이라고 합니다. 한 차원을 추가하여 표현한 것이기 때문에 우리는 Homogeneous Coordinate(동차 좌표계)를 사용합니다.

아핀 공간에 존재하는 점과 벡터의 관계는 다음과 같습니다.

assets 2021 08 30 1

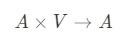
벡터는 눈에 보이지 않는 힘이며 점은 실질적인 물체를 의미합니다. 위의 수식을 보게되면 $A$ 라는 점이 $V$ 에 의해서 carry되는데 운반된 결과는 다시 점이 됩니다. 결국 점에 벡터를 연산하면 결국 점이 되며 이는 다음과 같은 3가지 특징을 만족하게 됩니다.

assets 2021 08 30 2

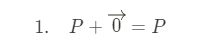
어떤 점에 영벡터를 더하게되면 해당 점이 나오게 됩니다. 아무런 힘이 작용하지 않았겠죠?

assets 2021 08 30 3

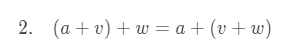
아핀 공간에서는 결합법칙이 성립됩니다.

assets 2021 08 30 4

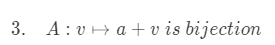
’↦‘란 어떤 함수가 왼쪽에 존재하는 원소를 오른쪽에 존재하는 원소로 mapping시킨다는 의미입니다. 위의 식을 보게 되면 $v$ 라는 원소를 $a+v$ 라는 원소로 mapping해주는함수 $A$ 가 존재하는데 해당 원소( $a, a+v)$ 가 정확히 1:1로 matching되기 때문에 $bijection$ 되었다고 말해주고 있습니다. 참고로 $bijection$ 이란 전단사를 의미하며 정의역 원소 하나에 하나의 공역 원소가 대응되며, 모든 공역의 원소들이 사용됩니다.🙂 즉, 점 element와 점+vector element는 1:1로 매칭되는 $bijection$ 이라는 이야기 입니다.

3번 특징을 해석을 해본다면 어떤 점 P에 벡터 $v$ 를 더하여 새로운 점 $Q$ 를 구했다고 했을 때 점 $Q$ 에서 점 $P$ 를 빼면 벡터 $v$ 를 만들 수 있다는 것을 의미합니다. 따라서 아핀 공간의 점과 벡터는 아래와 같은 성질을 가질 수 있습니다.

$dot$ $+$ $vector = dot$
$dot -dot=vector$
$dot -vector =dot$

지금까지 $vector$ 와 $dot$ 의 관계를 알아보았습니다. $vector$ 와 $dot$ 을 Affine Transformation에서 어떻게 활용하고 사용하는지 알아보도록 하겠습니다.

Affine Transformation

Linear transformation에서는 $vector$ 와 $dot$ 를 사용하여 affine transformation을 수행하게 되는데 형태를 linear transformation 형태인 $y=Ax$ 로 추려내기 위해서 노력을 하게 됩니다. 즉, point의 transformation과 vector의 transformation을 lienar transformation형태로( $y=Ax$ ) 합치기 위해서 Homogeneous Coordinate를 사용합니다. $vector$ 와 $dot$ 의 표기는 아래와 같습니다.

$vector= \begin{pmatrix} v_x\\ v_y\\ v_z\\ 0\\ \end{pmatrix} dot= \begin{pmatrix} p_x\\ p_y\\ p_z\\ 1\\ \end{pmatrix}$

위의 수식을 보게되면 $vector, dot$ 에 뒤에 숫자를 하나씩 더 붙혀서 4차원을 만들어주는 것을 볼 수 있습니다. 즉, n차원의 $vector$ 와 $dot$ 을 표현할 때 element가 n+1개인 column matrix 사용하게 되는 것입니다. 또한, 수식을 보면 알 수 있듯이 $vector$ 의 경우 아래에 0을 대입시켜주고, $dot$ 의 경우 아래에 1을 대입시켜 $vector$ 인지 $dot$ 인지 구분하게 됩니다.

이런 형태로 $vector$ 와 $dot$ 을 정의한다면 $y=Ax$ 형태로 정의할 수 있기 때문에 affine transformation을 linear transformation이라고 볼 수 있게 됩니다.

Affine transformation을 $y=Ax$ 형태로 나타낼 수 있는데 이 식에서 $A$ 를 affine transformation matrix라고 합니다. 이 matrix가 어떤 형태인지 따라서 기하학적으로 다른 의미를 갖습니다. 아래의 두 개의 affine transformation matrix를 살펴봅시다.

$\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\0 & 0 & 1\\ \end{pmatrix}$

위의 $A$ 를 사용하게 되면 첫 번째 열벡터와 두 번쨰 열벡터는 $vector$ 란 것을 알 수 있습니다. 이는 2차원에서의 2개의 기저벡터가 $\hat i=\begin{pmatrix}1 \\0 \end{pmatrix}$ , $\hat j=\begin{pmatrix}0 \\1 \end{pmatrix}$ 임을 의미합니다. $A$ 에서의 세번째 열벡터 $\begin{pmatrix} 0 \\0 \\1\end{pmatrix}$ 에서 세번째 element가 1이므로 point를 의미하게되는데 이 point $\begin{pmatrix} 0 \\0 \end{pmatrix}$ 은 벡터 공간의 원점을 의미한다고 볼 수 있습니다. 즉, $A$ 는 벡터 공간에서 $\begin{pmatrix} 0 \\0 \end{pmatrix}$ 을 원점으로 하며 기저벡터 $\hat i=\begin{pmatrix}1 \\0 \end{pmatrix}$ , $\hat j=\begin{pmatrix}0 \\1 \end{pmatrix}$ 을 갖는 matrix를 의미합니다. 기하학적으로 봤을 때, 이 $A$ matrix를 사용하게 되면 이미지에는 아무런 변화가 없게 됩니다. 원래의 이미지 원본이 $\begin{pmatrix} 0 \\0 \end{pmatrix}$ 을 원점으로 하고 기본이되는 기저벡터가 $\hat i=\begin{pmatrix}1 \\0 \end{pmatrix}$ , $\hat j=\begin{pmatrix}0 \\1 \end{pmatrix}$ 를 가지니까요!

다음은 이동을 시킬 수 있는 Translation 기능을 가진 affine transformation matrix를 살펴보도록 하겠습니다.

$\begin{pmatrix} 1 & 0 & X\\ 0 & 1 & Y\\0 & 0 & 1\\ \end{pmatrix}$

위의 matrix를 보게되면 기저벡터 $\hat i=\begin{pmatrix}1 \\0 \end{pmatrix}$ , $\hat j=\begin{pmatrix}0 \\1 \end{pmatrix}$ 을 갖고 원점이 $\begin{pmatrix} X \\Y \end{pmatrix}$ 인 새로운 벡터 공간이 생기게 됩니다. 원점이

$\begin{pmatrix} 0 \\0 \end{pmatrix}$ 에서 $\begin{pmatrix} X \\Y \end{pmatrix}$ 로 바뀌었기 때문에 $\begin{pmatrix} X \\Y \end{pmatrix}$ 만큼 translation한 것입니다.

assets 2021 08 30 5

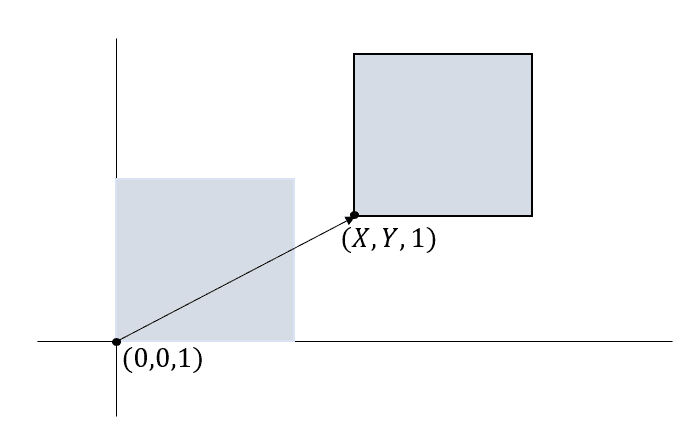
위의 그림은 아핀 공간에 존재하는 점(벡터 공간에서의 원점)을 이동한 그림입니다. $\begin{pmatrix}0 \\0 \\ 1\end{pmatrix}$ 을 $\begin{pmatrix}X \\Y \\ 1\end{pmatrix}$ 로 옮기기 위해서 아래와 같은 연산이 진행 됩니다.

$\begin{pmatrix} 1 & 0 & X\\ 0 & 1 & Y\\0 & 0 & 1\\ \end{pmatrix}\begin{pmatrix}0 \\0 \\ 1\end{pmatrix}=\begin{pmatrix}X \\Y \\ 1\end{pmatrix}$

위의 식을 보게되면 point를 이동행렬에 곱하면 point가 이동되는 것을 볼 수 있습니다. 하지만 벡터를 이동행렬에 곱하면 어떻게 될까요?

$\begin{pmatrix} 1 & 0 & X\\ 0 & 1 & Y\\0 & 0 & 1\\ \end{pmatrix}\begin{pmatrix}1 \\1 \\ 0\end{pmatrix}=\begin{pmatrix}1 \\1 \\ 0\end{pmatrix}$

직관적으로 벡터에 이동행렬을 곱하게되면 벡터를 이동시킬 수 없기 때문에 기존의 벡터가 그대로 나오게 됩니다. 하지만 왼쪽의 행렬에서 기저벡터를 바꿔주게 되면 linear transformation에서 얻을 수 있는 효과(shearing, rotation 등등)을 얻을 수 있습니다.

즉, affine transformation에서 translation(이동) 및 linear transformation의 효과를 얻기 위해서는 affine transformation matirx에 곱해지는 것을 $point$ 로 설정하면 되고, linear transformation의 효과만을 얻기 위해서는 $vector$ 로 설정하면 됩니다. 이 설명은 아래의 그림을 보게되면 잘 이해할 수 있습니다.

assets 2021 08 30 6

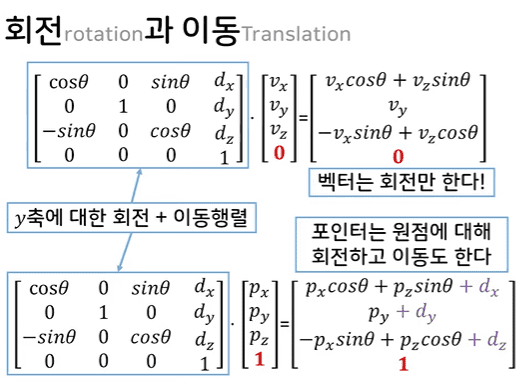
정리하자면, affine transformation은 추가적인 element를 사용하는 Homogeneous coordinate를 사용하여 linear transformation의 형태로 표현할 수 있습니다. 이에 linear vector space에서 할 수 있는 기하학적인 모든 동작을 수행 가능(linear transformation)하며 추가적으로 translation(이동)까지 가능합니다. 또한 affine transformation에서 사용하는 affine transformation matrix에 따라 작동되는 동작이 다르며 linear transformation만을 작동시키려면 affine transformation matrix에 $vector$ 를, translation까지 적용하려면 $point$ 를 matrix multiplication하면 됩니다.

The Feature of Affine Transformation

기하학적으로 봤을 때, 아래와 같은 특징을 만족합니다.

점, 직선, 면을 유지합니다.
평행선들은 변환 후에도 평행합니다.
직선 간의 각도나 포인트 사이이의 거리를 유지해주지는 않습니다. linear transformation도 마찬가지입니다.
같은 직선상의 포인트들 간의 거리 비율이 유지됩니다. 왜냐하면 기저벡터만을 바꾸고 상수배해주기 때문에 비율은 항상 상수배로 유지합니다.
다양한 변환이 가능합니다(translation + linear transformation)
좌표계 변환에도 많이 쓰인다고 합니다.

Homogeneous Coordinate

Affine 변환을 사용할 때 Homogeneous Coordinate를 사용하는 이유는 linear transformation으로 만들어주기 위함인데 이 원리는 다음과 같습니다.

assets 2021 08 30 7

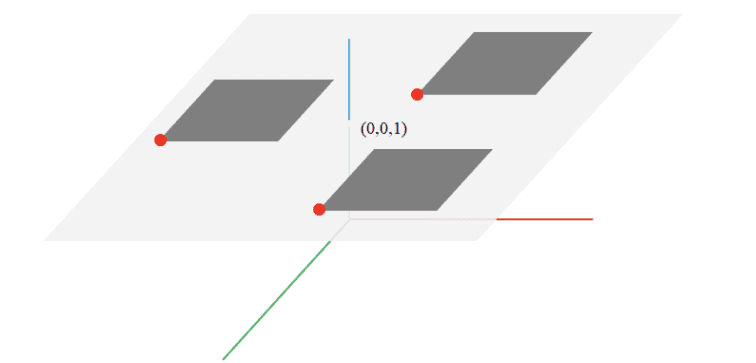
원래 생성 되는 벡터공간이 2차원인데 추가적으로 element를 하나 사용함으로써 3차원 공간 안에서 2차원 벡터 공간을 정의하게 됩니다. 위의 사진에서는 각각의 2차원 벡터 공간이 존재하는데 벡터 공간의 원점은 affine space의 point를 의미하게 되고 모든 점들은 $z=1$ 평면에 존재하게 됩니다. 벡터공간은 affine transformation matrix가 translation을 수행할 때 새롭게 생기게 되며 matrix에 의해 $\begin{pmatrix}X \\Y \end{pmatrix}$ 만큼 평행이동한다고 생각했을 때 벡터공간의 원점이 $\begin{pmatrix}X \\Y \end{pmatrix}$ 만큼 평행이동했다고 생각할 수 있습니다. 이렇게 새로운 element하나를 추가하고 그 차원의 값을 1로 고정하여 점들을 나타내므로써 3차원에서 2차원을 표현할 수 있게 되는 것입니다.

Summary

벡터는 나타낼 수 없으며 점을 이동시키는 하나의 수단입니다.
이런 벡터와 점을 나타내는 차원을 하나 추가하여 2차원을 3차원안에서 표현하는 Homogeneous Coordinate를 사용합니다.
Affine transformation은 translation 및 linear transformation이 가능합니다.
벡터 공간에서의 원점은 affine space에서의 점과 대응됩니다.
Affine transformation matrix와 $vector$ 를 곱하게 되면 linear transformation을 구현할 수 있고 $point$ 를 곱하게 되면 translation 및 linear transformation을 구현할 수 있습니다.
$\begin{pmatrix} 1 & 0 & X\\ 0 & 1 & Y\\0 & 0 & 1\\ \end{pmatrix}$ 가 affine transformation matrix라고 했을 때, $\begin{pmatrix} 1 & 0 \\ 0 & 1 & \\0 & 0 \\ \end{pmatrix}$ 은 두 개의 (변형된)기저 벡터를 의미하며 $\begin{pmatrix} X\\ Y\\ 1\\ \end{pmatrix}$ 는 이동(벡터 공간의 원점)을 의미합니다. 그리고 이동을 하기 위해선 이 matrix에 $point$ ( 예를 들어, $\begin{pmatrix} 2\\ 2\\ 1\\ \end{pmatrix}$ ⇒두 개의 기저 벡터가 $\begin{pmatrix} 1 \\ 0 \\ \end{pmatrix}$ , $\begin{pmatrix} 0 \\ 1 \end{pmatrix}$ 일 경우, (2,2)였던 지점을 $X,Y$ 만큼 이동)를 곱하면 됩니다.